Sorting 2 - Challenges
Download exercises zip
Crime parade
A bank robbery has been committed, and witnesses gave police the description of a gangster as a series of \(m\) features. For us all features are just numbers, you do not need to care about their range:
# height weight beard moustache eye color (RGB)
[ 1.70, 80, 0, 1, 190,150,230 ]
The police then caught a bunch of \(n\) usual suspects and gathered them in the waiting room of the police station. Witnesses will be asked to recognize the actual gangster among a lineup of criminals who are deemed most similar in features to the description. To fill the lineup, the policeman will:
go to the waiting room and select the criminal most distant from the description
bring the criminal at the right of the lineup
repeat until there are no more criminals in the waiting room
Write a function lineup which takes a dictionary of gangster nicknames mapped to their features and a suspect description as a list of features. To implement it, create two lists lineup_names and lineup_sims of fixed length set equal to the number of criminals. Fill the lists with empty strings. Then implement the algorithm as a kind of selection sort, where you keep filling the lists cells always writing into the first available cell found from the left, printing at each step
what happens as in the example. Note our version would not be an in-place algorithm, as we are creating new lists to host the data.
you can assume max name length is
9
Implement this support function to calculate distance among two criminals (it’s the square root of sum of squared differences):
def distance(features1, features2):
""" Takes two lists, each having m features as floats
and RETURN a float which is the vector distance among
the two features
- MUST RUN IN O(m) WHERE m IS THE NUMBER OF FEATURES
"""
implement main
lineupfunction:
def lineup(waiting_room, description):
""" RETURN a NEW list of the criminals names sorted by similarity distance with description,
from most distant to least distant
PRINT all the passages
MODIFY waiting_room so it's empty at the end
"""
DO NOT recalculate distance each time you have to compare suspects with the description, that would be an unacceptable extra \(O(n m)\) cost. Instead, save somewhere the distance of each suspect so you can get it fast later
DO NOT change length of lists (so no .insert, .remove(), .pop(), .append,.extend, …), you can only set cell values of lineup_names and lineup_sims!
DO NOT call min, max, sum
DO NOT call sort() nor sorted() - seems obvious, but during exams there were people who called it in exercises about sorting (they didn’t get a good grade)
Testing: python3 -m unittest sorting_chal_test.TestLineup
[2]:
from sorting_chal_sol import *
waiting_room = { # height weight beard moustache eye color (RGB)
'The Saint': [1.70, 90, 1, 0, 250,100,190],
'Goliath': [2.00, 120, 0, 0, 210,230, 30],
'Revolvers': [1.80, 70, 1, 1, 40,120, 30],
'Mammoth': [1.60, 60, 1, 0, 110,230, 30],
'Razor': [1.80, 110, 1, 0, 130,230, 20],
'Shadow': [1.60, 70, 1, 0, 190,230,140],
'Moneybags': [1.60, 80, 1, 0, 210,230,220],
'Bomber': [1.70, 100, 0, 0, 140,110,170],
'Rifleman': [1.60, 90, 1, 1, 110, 20, 40],
'The Ghost': [1.60, 50, 0, 0, 150, 70, 90]
}
lineup(waiting_room, [1.70, 80, 0, 1, 190,150,230 ])
Waiting room: The Saint,Goliath,Revolvers,Mammoth,Razor,Shadow,Moneybags,Bomber,Rifleman,The Ghost
Most distant is Revolvers with distance 251.99 , moving him into the lineup
| 251.99| | | | | | | | | |
|Revolvers| | | | | | | | | |
Waiting room: The Saint,Goliath,Mammoth,Razor,Shadow,Moneybags,Bomber,Rifleman,The Ghost
Most distant is Rifleman with distance 243.93 , moving him into the lineup
| 251.99| 243.93| | | | | | | | |
|Revolvers| Rifleman| | | | | | | | |
Waiting room: The Saint,Goliath,Mammoth,Razor,Shadow,Moneybags,Bomber,The Ghost
Most distant is Razor with distance 234.53 , moving him into the lineup
| 251.99| 243.93| 234.53| | | | | | | |
|Revolvers| Rifleman| Razor| | | | | | | |
Waiting room: The Saint,Goliath,Mammoth,Shadow,Moneybags,Bomber,The Ghost
Most distant is Mammoth with distance 230.66 , moving him into the lineup
| 251.99| 243.93| 234.53| 230.66| | | | | | |
|Revolvers| Rifleman| Razor| Mammoth| | | | | | |
Waiting room: The Saint,Goliath,Shadow,Moneybags,Bomber,The Ghost
Most distant is Goliath with distance 220.00 , moving him into the lineup
| 251.99| 243.93| 234.53| 230.66| 220.00| | | | | |
|Revolvers| Rifleman| Razor| Mammoth| Goliath| | | | | |
Waiting room: The Saint,Shadow,Moneybags,Bomber,The Ghost
Most distant is The Ghost with distance 168.82 , moving him into the lineup
| 251.99| 243.93| 234.53| 230.66| 220.00| 168.82| | | | |
|Revolvers| Rifleman| Razor| Mammoth| Goliath|The Ghost| | | | |
Waiting room: The Saint,Shadow,Moneybags,Bomber
Most distant is Shadow with distance 120.84 , moving him into the lineup
| 251.99| 243.93| 234.53| 230.66| 220.00| 168.82| 120.84| | | |
|Revolvers| Rifleman| Razor| Mammoth| Goliath|The Ghost| Shadow| | | |
Waiting room: The Saint,Moneybags,Bomber
Most distant is Bomber with distance 90.01 , moving him into the lineup
| 251.99| 243.93| 234.53| 230.66| 220.00| 168.82| 120.84| 90.01| | |
|Revolvers| Rifleman| Razor| Mammoth| Goliath|The Ghost| Shadow| Bomber| | |
Waiting room: The Saint,Moneybags
Most distant is The Saint with distance 88.33 , moving him into the lineup
| 251.99| 243.93| 234.53| 230.66| 220.00| 168.82| 120.84| 90.01| 88.33| |
|Revolvers| Rifleman| Razor| Mammoth| Goliath|The Ghost| Shadow| Bomber|The Saint| |
Waiting room: Moneybags
Most distant is Moneybags with distance 83.08 , moving him into the lineup
| 251.99| 243.93| 234.53| 230.66| 220.00| 168.82| 120.84| 90.01| 88.33| 83.08|
|Revolvers| Rifleman| Razor| Mammoth| Goliath|The Ghost| Shadow| Bomber|The Saint|Moneybags|
[2]:
['Revolvers',
'Rifleman',
'Razor',
'Mammoth',
'Goliath',
'The Ghost',
'Shadow',
'Bomber',
'The Saint',
'Moneybags']
McFat’s
The fastfood chain MacFat’s recently opened new stores around main attractions of each major Italian city: even if not economically profitable (obviously, you can’t compete with Italian food), the flashy store signs will get featured in the thousands pictures turists take each day, and will appear in the many reports tv networks give daily from main squares.
Each store can hold up to n people in a queue. McFat’s rewards obese clients by assigning them a priority according to their weight, so overweights clients can go past thinner ones. If a client has the same weight as another one, he/she will queue just behind the client who arrived first.
Write a function mcfats which shows a queue of a list of clients, where each client is represented as an integer indicating his/her weight. In the function, create two zero-filled lists arrival_times and weigths of fixed length set equal to the number of clients. Then implement the algorithm as a kind of insertion sort, where you keep filling the lists cells from the left, printing at each step what happens as in the example. Note our version would not be an in-place algorithm,
as we are creating new lists to host the data.
def mcfats(clients):
""" RETURN a NEW sorted list with the client weights, from smallest to greatest
PRINT all the passages
DO *NOT* MODIFY clients
"""
First client arrives at time
1Display zeros as empty spaces
DO NOT change length of lists (so no .insert, .remove(), .pop(), .append,.extend, …), you can only set cell values of arrival_times and weigths!
DO NOT call min, max, sum
DO NOT call sort() nor sorted() - seems obvious, but during exams there were people who called it in exercises about sorting (they didn’t get a good grade)
Testing: python3 -m unittest sorting_chal_test.TestMcFats
[3]:
from sorting_chal_sol import *
[4]:
# 9, 8, 7, 6, 5, 4, 3, 2, 1 # arrival time
cs = [80,90,50,60,80,60,80,50,70]
res = mcfats(cs)
print(res)
assert cs == [80,90,50,60,80,60,80,50,70] # don't sort original
assert res == [50,50,60,60,70,80,80,80,90] # return a new sorted version
weight 70 kg arrived at time 1
will insert in slot = 0
no people to shift
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 1| | | | | | | | |
weights: |70| | | | | | | | |
weight 50 kg arrived at time 2
will insert in slot = 0
will shift 1 people starting from slot 0
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 2| 1| | | | | | | |
weights: |50|70| | | | | | | |
weight 80 kg arrived at time 3
will insert in slot = 2
no people to shift
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 2| 1| 3| | | | | | |
weights: |50|70|80| | | | | | |
weight 60 kg arrived at time 4
will insert in slot = 1
will shift 2 people starting from slot 1
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 2| 4| 1| 3| | | | | |
weights: |50|60|70|80| | | | | |
weight 80 kg arrived at time 5
will insert in slot = 3
will shift 1 people starting from slot 3
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 2| 4| 1| 5| 3| | | | |
weights: |50|60|70|80|80| | | | |
weight 60 kg arrived at time 6
will insert in slot = 1
will shift 4 people starting from slot 1
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 2| 6| 4| 1| 5| 3| | | |
weights: |50|60|60|70|80|80| | | |
weight 50 kg arrived at time 7
will insert in slot = 0
will shift 6 people starting from slot 0
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 7| 2| 6| 4| 1| 5| 3| | |
weights: |50|50|60|60|70|80|80| | |
weight 90 kg arrived at time 8
will insert in slot = 7
no people to shift
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 7| 2| 6| 4| 1| 5| 3| 8| |
weights: |50|50|60|60|70|80|80|90| |
weight 80 kg arrived at time 9
will insert in slot = 5
will shift 3 people starting from slot 5
slot: | 0| 1| 2| 3| 4| 5| 6| 7| 8|
arrival_times:| 7| 2| 6| 4| 1| 9| 5| 3| 8|
weights: |50|50|60|60|70|80|80|80|90|
[50, 50, 60, 60, 70, 80, 80, 80, 90]
Partitocracy
A democracy degenerates into a partitocracy when political parties keep splitting the power among themselves without actually allowing citizens to have their say. Parties pretend there is a lively democracy by being very litigious, and keep creating factions this way:
1 - at the beginning there are all the people, each with a number indicating his/her political inclination:
We, the people: [6, 3, 5, 7, 5, 7, 2, 9, 1, 4, 8]
2 - the people elect a leader - as thoughtful criteria they of course choose the first guy who passes by:
- elect our new leader: 6
3 - heated arguments around the leader begin: people leaning left of him/her decide to create their own party:
- create a new left party: [3, 5, 5, 2, 1, 4]
while right-leaning people (or with equal orientation) create their own party:
- create a new right party: [7, 7, 9, 8]
Naturally, both parties recursively degenerate into their own partitocracies.
4 - the leader feels ignored by the original voters, so in protest creates his/her own party of one person
5 - a new partitocracy is produced, by joining left partitocracy with the one-person party of the leader and the right partitocracy:
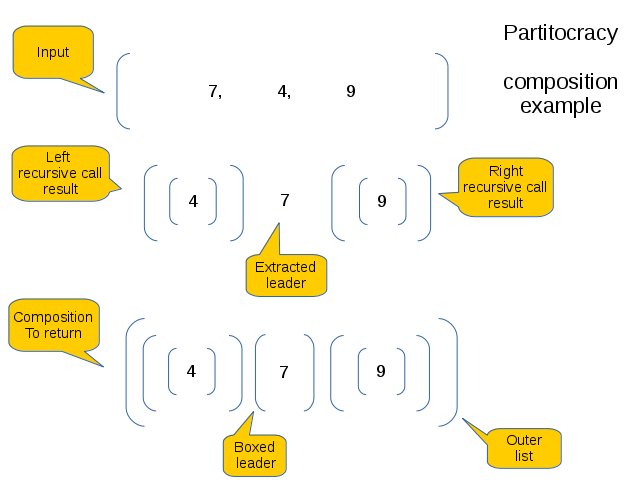
- join them in a new partitocracy: [[[[[1]], [2]], [3], [[[4]], [5], [[5]]]], [6], [[7], [[7], [[[8]], [9]]]]]
The result is of course a mess of burocratic structures. If we pprint with width=10 the result, the subdivision is slighlty clearer:
[[[[[1]], <---- left partitocracy
[2]],
[3],
[[[4]],
[5],
[[5]]]],
[6], <---- leader
[[7], <---- right partitocracy
[[7],
[[[8]],
[9]]]]]
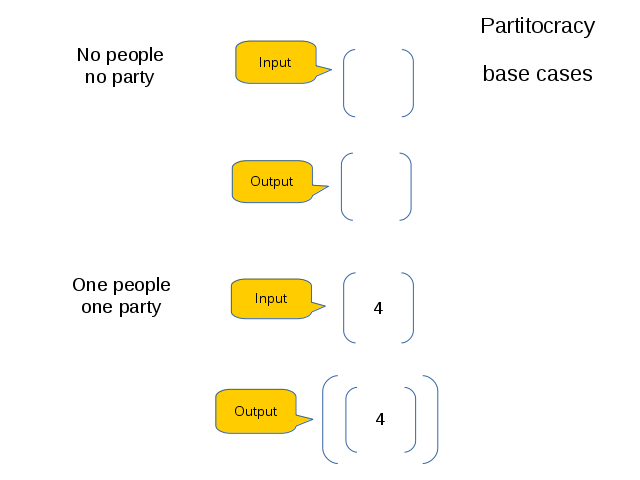
Implement the following function, which is a kind of quick sort, although this version does not modify input data so it is not in-place:
def partitocracy(people, level=0):
"""Takes a list of integers and:
PRINT the process, starting each line with a number
of spaces proportional to recursion level parameter
RETURN a partitocracy as a NEW list of nested lists
- a recursive implementation is acceptable
"""
MUST execute in \(O(n \log{n})\) where \(n\) is the size of the input list. Note that since this is a kind of quick sort, the actual worst time (when the list is already sorted) would be \(O(n^2)\), but in most cases it performs in \(O(n \log{n})\)
DO NOT modify the input list
ONLY USE .append method to change lists size
DO NOT append empty lists to a partitocracy
DO NOT call min, max, sum
DO NOT call sort() nor sorted() - seems obvious, but during exams there were people who called it in exercises about sorting (they didn’t get a good grade)
Testing: python3 -m unittest sorting_chal_test.TestPartitocracy
[5]:
from sorting_chal_sol import partitocracy
italy = [6,3,5,7,5,7,2,9,1,4,8]
res = partitocracy(italy)
from pprint import pprint
print()
print()
print('Result pprint is:')
print()
pprint(res, width=10)
We, the people: [6, 3, 5, 7, 5, 7, 2, 9, 1, 4, 8]
- elect our new leader: 6
- create a new left party: [3, 5, 5, 2, 1, 4]
We, the people: [3, 5, 5, 2, 1, 4]
- elect our new leader: 3
- create a new left party: [2, 1]
We, the people: [2, 1]
- elect our new leader: 2
- create a new left party: [1]
We, the people: [1]
- elect our new leader: 1
- can't create a left party
- can't create a right party
- join them in a new partitocracy: [[1]]
- can't create a right party
- join them in a new partitocracy: [[[1]], [2]]
- create a new right party: [5, 5, 4]
We, the people: [5, 5, 4]
- elect our new leader: 5
- create a new left party: [4]
We, the people: [4]
- elect our new leader: 4
- can't create a left party
- can't create a right party
- join them in a new partitocracy: [[4]]
- create a new right party: [5]
We, the people: [5]
- elect our new leader: 5
- can't create a left party
- can't create a right party
- join them in a new partitocracy: [[5]]
- join them in a new partitocracy: [[[4]], [5], [[5]]]
- join them in a new partitocracy: [[[[1]], [2]], [3], [[[4]], [5], [[5]]]]
- create a new right party: [7, 7, 9, 8]
We, the people: [7, 7, 9, 8]
- elect our new leader: 7
- can't create a left party
- create a new right party: [7, 9, 8]
We, the people: [7, 9, 8]
- elect our new leader: 7
- can't create a left party
- create a new right party: [9, 8]
We, the people: [9, 8]
- elect our new leader: 9
- create a new left party: [8]
We, the people: [8]
- elect our new leader: 8
- can't create a left party
- can't create a right party
- join them in a new partitocracy: [[8]]
- can't create a right party
- join them in a new partitocracy: [[[8]], [9]]
- join them in a new partitocracy: [[7], [[[8]], [9]]]
- join them in a new partitocracy: [[7], [[7], [[[8]], [9]]]]
- join them in a new partitocracy: [[[[[1]], [2]], [3], [[[4]], [5], [[5]]]], [6], [[7], [[7], [[[8]], [9]]]]]
Result pprint is:
[[[[[1]],
[2]],
[3],
[[[4]],
[5],
[[5]]]],
[6],
[[7],
[[7],
[[[8]],
[9]]]]]
HINT: To solve it, first consider base cases, then how to compose them, and finally generalize: