Sorting 1 - intro
Download exercises zip
Introduction
We will see several algorithms for sorting and discuss their time and space complexity along the way.
BEFORE CONTINUING, READ FIRST THE WORKSHEETS ON RECURSION AND ON ALGORITHM ANALYSIS
References
Erik Dassi’s Algorithm analysis slides 1 and 2, sorting
Python DS Chapter 2.6: Algorithm analysis
What to do
unzip exercises in a folder, you should get something like this:
sorting
sorting.ipynb
insertion_sort.py
insertion_sort_test.py
insertion_sort_sol.py
selection_sort.py
selection_sort_test.py
selection_sort_sol.py
jupman.py
sciprog.py
.
.
.
open the editor of your choice (for example Visual Studio Code, Spyder or PyCharme), you will edit the files ending in
.pyfilesGo on reading this notebook, and follow instuctions inside.
Exercises
1 Selection Sort
We will try to implement Selection Sort on our own. Don’t look at existing solutions. In this exercises, you will only be allowed to look at this picture:

Image credits: dr Alberto Montresor
To start with, open selection_sort.py in an editor of your choice.
Now proceed reading.
1.1 Implement swap
[2]:
def swap(A, i, j):
""" MODIFIES the array A by swapping the elements at position i and j
"""
raise Exception("TODO implement me!")
In order to succeed in this part of the course, you are strongly invited to first think hard about a function, and then code! So to start with, pay particular attention at the required inputs and expected outputs of functions. Before start coding, answer these questions:
QUESTION 1.1.1: What are the input types of swap? In particular
What is the type of the elements in
A?Can we have both strings and floats inside
A?
What is the type of
iandj?
VII COMMANDMENT: You shall also write on paper!
Help yourself by drawing a representation of input array. Staring at the monitor doesn’t always work, so help yourself and draw a representation of the state sof the program. Tables, nodes, arrows, all can help figuring out a solution for the problem.
QUESTION 1.1.2: What should be the result of the three prints here? Should the function swap return something at all ? Try to answer this question before proceeding.
A = ['a','b','c']
print(A)
print(swap(A, 0, 2))
print(A)
HINT: Remember this:
VI COMMANDMENT You shall use return command only if you see written RETURN in the function description!
If there is no return in function description, the function is intended to return None.
QUESTION 1.1.3: Try to answer this question before proceeding:
What is the result of the first and second print down here?
What is the result of the final print if we have arbitrary indeces \(i\) and \(j\) with \(0 \leq i,j \leq 2\) ?
A = ['a','b','c']
swap(A, 0, 2)
print(A)
swap(A, 2, 0)
print(A)
QUESTION 1.1.4: What is the result of the final print here? Try to answer this question before proceeding:
A = ['a','b','c']
swap(A, 1, 1)
print(A)
QUESTION 1.1.5:
In the same file
selection_sort.pycopy at the end the test code at the end of this question.Read carefully all the test cases, in particular
test_swap_propertyandtest_double_swap. They show two important properties of the swap function that you should have discovered while ansering the questions before.Why should these tests succeed with implemented code? Make sure to answer.
EXERCISE: implement swap
Proceed implementing the swap function
To test the function, run:
python3 -m unittest selection_sort_test.SwapTest
Notice that:
In the command above there is no
.pyat the end ofselection_sort_testWe are executing the command in the operating system shell, not Python (there must not be
>>>at the beginning)At the end of the filename, there is a dot followed by a test class name
SwapTest, which means Python will only execute tests contained inSwapTest. Of course, in this case those are all the tests we have, but if we add many test classes to our file, it will be useful to able to filter executed tests.According to your distribution (i.e. Anaconda), you might need to write
pythoninstead ofpython3
QUESTION 1.1.6: Read Error kinds section in Testing. Suppose you will be the only one calling swap, and you suspect your program somewhere is calling swap with wrong parameters. Which kind of error would that be? Add to swap some appropriate precondition checking.
1.2 Implement argmin
Try to code and test the partial argmin pos function:
[3]:
def argmin(A, i):
""" RETURN the *index* of the element in list A which is lesser than or equal
to all other elements in A that start from index i included
- MUST execute in O(n) where n is the length of A
"""
raise Exception("TODO implement me!")
QUESTION 1.2.1: What are the input types of argmin? In particular
What could be the type of the elements in
A?Can we have both strings and floats inside
A?
What is the type of
i?What is the range of
i?
QUESTION 1.2.2: Should the function argmin return something ? What would be the result type? Try to answer this question before proceeding.
QUESTION 1.2.3: Look again at the selection_sort matrix, and compare it to the argmin function definition:

Can you understand the meaning of orange and white boxes?
What does the yellow box represent?
QUESTION 1.2.4:
Draw a matrix like the above for the array
A = ['b','a','c'], adding the corresponding row and column numbers foriandjWhat should be the result of the three prints here?
A = ['a','b','c']
print(argmin(A,0))
print(argmin(A,1))
print(argmin(A,2))
print(A)
EXERCISE 1.2.5: Copy the following test code at the end of the file selection_sort.py, and start coding a solution.
To test the function, run:
python3 -m unittest selection_sort_test.ArgminTest
Notice how now we are appending .ArgminTest at the end of the command.
Warning: Don’t use slices ! Remember their computational complexity, and that in these labs we do care about performances!
1.3: Full selection_sort

Let’s talks about implementing selection_sort function in selection_sort.py
[4]:
def selection_sort(A):
""" Sorts the list A in-place in O(n^2) time this ways:
1. Looks at minimal element in the array [i:n],
and swaps it with first element.
2. Repeats step 1, but considering the subarray [i+1:n]
Remember selection sort has complexity O(n^2) where n is the
size of the list.
"""
raise Exception("TODO implement me!")
Note: on the book website there is an implementation of the selection sort with a nice animated histogram showing a sorting process. Differently from the slides, instead of selecting the minimal element the algorithm on the book selects the maximal element and puts it to the right of the array.
QUESTION 1.3.1:
What is the expected return type? Does it return anything at all?
What is the meaning of ‘Sorts the list A in-place’ ?
QUESTION 1.3.2:
At the beginning, which array indeces are considered?
At the end, which array indeces are considered ? Is
A[len(A) - 1:len(A)]ever considered ?
EXERCISE 1.3.3:
Try now to implement selection_sort in selection_sort.py, using the two previously defined functions swap and argmin.
HINT: If you are having troubles because your selection sort passes wrong arguments to either swap or argmin, feel free to add further assertions to both. They are much more effective than prints !
To test the function, run:
python3 -m unittest selection_sort_test.SelectionSortTest
2 Insertion sort
Insertion sort is a basic sorting algorithm. This animation gives you an idea of how it works
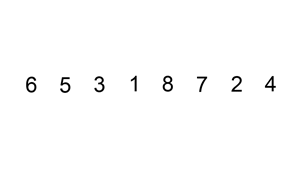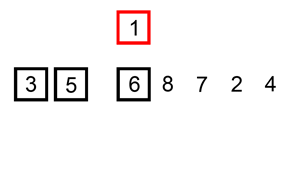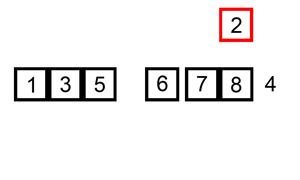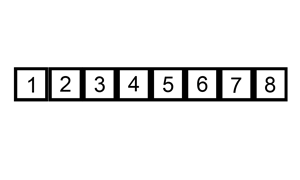
From the animation, you can see these things are going on:
The red square selects one number starting from the leftomost (question: does it actually need to be the leftmost ? Can we save one iteration?). Let’s say it starts at position
i.While the number in the red square is lesser then the previous one, it is shifted back one position at a time
The red square now selects the number immediately following the previous starting point of the red square, that is, selects position
i + 1
From the analysis above:
how many cycles do we need ? One, Two, Three?
Are they nested?
Is there one cycle with a fixed number of iterations ? Is there one with an unknown number of iterations?
What is the worst-case complexity of the algorithm?
As always, if you have troubles finding a generic solution, take a fixed list and manually write down all the steps to do the algorithm. Here we give a sketch:
# i=0,1,2,3,4,5
A = [3,7,8,9,6,2]
Let’s say we have red square at i=4
i = 4
red = A[4] # in red we put the value in A[4] which is 6
# 0,1,2,3,4,5
# [3,7,8,9,6,2] start
A[4] = A[3] # [3,7,8,9,9,2]
A[3] = A[2] # [3,7,8,8,9,2]
A[2] = A[1] # [3,7,7,8,9,2]
A[1] = red # [3,6,7,8,9,2] A[1] < red, stop
We can generalize A index with a j:
i = 4
red = A[4]
j = 4
while ...
A[j] = A[j-1]
j -= 1
A[j] = red
Start editing the file insertion_sort.py and implement insertion_sort without looking at theory slides.
def insertion_sort(A):
""" Sorts in-place list A with insertion sort
"""
3 Merge sort
With merge sort we model lists to ordered as stacks, so it is important to understand how to take elements from the end of a list and how to reverse a list to change its order.
Taking last element
To take last element from a list you may use [-1]:
[5]:
[9,7,8][-1]
[5]:
8
Reversing a list
REMEMBER: .reverse() method MODIFIES the list it is called on and returns None !
[6]:
lst = [9,7,8]
lst.reverse()
Notice how above Jupyter did not show anything, because implicitly the result of the call was None. Still, we have an effect, lst is now reversed:
[7]:
lst
[7]:
[8, 7, 9]
If you want to reversed version of a list without actually changing it, you can use reversed function:
[8]:
lst = [9,7,8]
reversed(lst)
[8]:
<list_reverseiterator at 0x7f95d2a6a210>
The returned value is an iterator, so something which is able to produce a reversed version of the list but it is still not a list. If you actually want to get back a list, you need to explicitly cast it to list:
[9]:
lst = [9,7,8]
list(reversed(lst))
[9]:
[8, 7, 9]
Notice lst itself was not changed:
[10]:
lst
[10]:
[9, 7, 8]
Removing last element with .pop()
To remove an element, you can use .pop() method, which does two things:
if not given any argument, removes the last element in \(O(1)\) time
returns it to the caller of the method, so for example we can conveniently store it in a variable
[11]:
A = [9,7,8]
x = A.pop()
[12]:
print(A)
[9, 7]
[13]:
print(x)
8
WARNING: internal deletion is expensive !
If you pay attention to performance (and in this course part you are), whenever you have to remove elements from a Python list be very careful about the complexity! Removal at the end is a very fast O(1), but internal removal is O(n) !
Costly internal del
You can remove an internal element with del
NOTE: del returns None
[14]:
lst = [9,5,6,7]
del lst[2] # internal delete is O(n)
[15]:
lst
[15]:
[9, 5, 7]
Costly internal pop
You can remove an internal element with pop(i)
[16]:
lst = [9,5,6,7]
lst.pop(2) # internal pop is O(n)
[16]:
6
[17]:
lst
[17]:
[9, 5, 7]
3.1 merge 1
Start editing merge_sort.py
merge1 takes two already ordered lists of size n and m and return a new one made with the elements of both in \(O(n+m)\) time. For example:
[18]:
from merge_sort_sol import *
merge1([3,6,9,13,15], [2,4,8,9])
[18]:
[2, 3, 4, 6, 8, 9, 9, 13, 15]
To implement it, keep comparing the last elements of the two lists, and at each round append the greatest in a temporary list, which you shall return at the end of the function (remember to reverse it!).
Example:
If we imagine the numbers as ordered card decks, we can picture them like this:
2 15
4 13
4 10
6 9
15 8 8
13 10 9 6
9 8 10 4
6 4 13 4
4 2 15 2
A B TMP RESULT
As Python lists, they would look like:
A=[4,6,9,13,15]
B=[2,4,8,10]
TMP=[15,13,10,9,8,6,4,4,2]
RESULT=[2,4,4,6,8,9,10,13,15]
The algorithm would:
compare 15 and 10, pop 15 and put it in TMP
compare 13 and 10, pop 13 and put it in TMP
compare 9 and 10, pop 10 and put it in TMP
compare 9 and 8, pop 9 and put it in TMP
etc …
finally return a reversed TMP
It remains to decide what to do when one of the two lists remains empty, but this is up to you.
To test:
python3 -m unittest merge_sort_test.Merge1Test
3.2 merge2
merge2 takes A and B as two ordered lists (from smallest to greatest) of (possibly negative) integers. Lists are of size n and m respectively, and RETURN a NEW list composed of the items in A and B ordered from smallest to greatest
MUST RUN IN \(O(m+n)\)
in this version, do NOT use
.pop()on input lists to reduce their size. Instead, use indeces to track at which point you are, starting at zero and putting minimal elements in result list, so this time you don’t even need a temporary list.
8 15
7 13
6 10
5 9
4 15 8
3 13 10 6
2 9 8 4
1 6 4 4
0 4 2 2
index A B RESULT
Sketch:
set i=0 (left index) and j=0 (right index)
compare 4 and 2, put 2 in RESULT, set i=0, j=1
compare 4 and 4, put 4 in RESULT, set i=1, j=1
compare 6 and 4, put 4 in RESULT, set i=1, j=2
compare 6 and 8, put 6 in RESULT, set i=2, j=2
etc …
finally return RESULT
To test:
python3 -m unittest merge_sort_test.Merge2Test
4 quick sort
Quick sort is a widely used sorting algorithm and in this exercise you will implement it following the pseudo code.
IMPORTANT: Array A in the pseudo code has indexes starting from zero included
IMPORTANT: The functions pivot and quicksort operate an a subarray that goes from indeces first included and last included !!!
Start editing the file quick_sort.py:
4.1 pivot
Try look at this pseudocode and implement pivot method.
IMPORTANT: If something goes wrong (it will), find the problem using the debugger !

def pivot(A, first, last):
""" MODIFIES in-place the slice of the array A with indeces between first included
and last **included**. RETURN the new pivot index.
"""
raise Exception("TODO IMPLEMENT ME!")
You can run tests only for pivot with this command:
python3 -m unittest quick_sort_test.PivotTest
4.2 quicksort and qs
Implement quicksort and qs method:

def quicksort(A, first, last):
"""
Sorts in-place the slice of the array A with indeces between
first included and last included.
"""
raise Exception("TODO IMPLEMENT ME !")
def qs(A):
"""
Sorts in-place the array A by calling quicksort function on the
full array.
"""
raise Exception("TODO IMPLEMENT ME !")
You can run tests only for both quicksort and qs with this command:
python3 -m unittest quick_sort_test.QuicksortTest
5 SwapArray
NOTE: This exercise was given at an exam. Solving it could have been quite easy, if students had just read the book (which is available when doing the exam)!
Interpret it as a warning that reading these worksheets alone is not enough to pass the exam.
You are given a class SwapArray that models an array where the only modification you can do is to swap an element with the successive one.
[19]:
from swap_array_sol import *
To create a SwapArray, just call it passing a python list:
[20]:
sarr = SwapArray([7,8,6])
print(sarr)
SwapArray: [7, 8, 6]
Then you can query in \(O(1)\) it by calling get() and get_last()
[21]:
sarr.get(0)
[21]:
7
[22]:
sarr.get(1)
[22]:
8
[23]:
sarr.get_last()
[23]:
6
You can know the size in \(O(1)\) with size() method:
[24]:
sarr.size()
[24]:
3
As we said, the only modification you can do to the internal array is to call swap_next method:
def swap_next(self, i):
""" Swaps the elements at indeces i and i + 1
If index is negative or greater or equal of the last index, raises
an IndexError
"""
For example:
[25]:
sarr = SwapArray([7,8,6,3])
print(sarr)
SwapArray: [7, 8, 6, 3]
[26]:
sarr.swap_next(2)
print(sarr)
SwapArray: [7, 8, 3, 6]
[27]:
sarr.swap_next(0)
print(sarr)
SwapArray: [8, 7, 3, 6]
Now start editing the file swap_array.py:
5.1 is_sorted
Implement the is_sorted function, which is a function external to the class SwapArray:
def is_sorted(sarr):
""" Returns True if the provided SwapArray sarr is sorted, False otherwise
NOTE: Here you are a user of SwapArray, so you *MUST NOT* access
directly the field _arr.
NOTE: MUST run in O(n) where n is the length of the array
"""
raise Exception("TODO IMPLEMENT ME !")
Once done, running this will run only the tests in IsSortedTest class and hopefully they will pass.
python3 -m unittest swap_array_test.IsSortedTest
Example usage:
[28]:
is_sorted(SwapArray([8,5,6]))
[28]:
False
[29]:
is_sorted(SwapArray([5,6,6,8]))
[29]:
True
5.2 max_to_right
Implement max_to_right function, which is a function external to the class SwapArray. There are two ways to implement it, try to minimize the reads from the SwapArray.
def max_to_right(sarr,i):
""" Modifies the provided SwapArray sarr so that its biggest element
in the subarray from 0 to i is moved at index i.
Elements *after* i are *not* considered.
The order in which the other elements will be after a call
to this function is left unspecified (so it could be any).
NOTE: Here you are a user of SwapArray, so you *MUST NOT* access
directly the field _arr. To do changes, you can only use
the method swap_next(self, i).
NOTE: does *not* return anything!
NOTE: MUST run in O(n) where n is the length of the array
"""
Testing: python3 -m unittest swap_array_test.MaxToRightTest
Example usage:
[30]:
sarr = SwapArray([7, 9, 6, 5, 8])
print(sarr)
SwapArray: [7, 9, 6, 5, 8]
[31]:
max_to_right(sarr,4) # 4 is an *index*
print(sarr)
SwapArray: [7, 6, 5, 8, 9]
[32]:
sarr = SwapArray([7, 9, 6, 5, 8])
print(sarr)
SwapArray: [7, 9, 6, 5, 8]
[33]:
max_to_right(sarr,3)
print(sarr)
SwapArray: [7, 6, 5, 9, 8]
[34]:
sarr = SwapArray([7, 9, 6, 5, 8])
print(sarr)
SwapArray: [7, 9, 6, 5, 8]
[35]:
max_to_right(sarr,1)
print(sarr)
SwapArray: [7, 9, 6, 5, 8]
[36]:
sarr = SwapArray([7, 9, 6, 5, 8])
print(sarr)
SwapArray: [7, 9, 6, 5, 8]
[37]:
max_to_right(sarr,0) # changes nothing
print(sarr)
SwapArray: [7, 9, 6, 5, 8]
5.3 swapsort
When you know how to push a maximum element to the rightmost position of an array, you almost have a sorting algorithm. So now you can try to implement swapsort function, taking inspiration from max_to_right. Note swapsort is a function external to the class SwapArray:
def swapsort(sarr):
""" Sorts in-place provided SwapArray.
NOTE: Here you are a user of SwapArray, so you *MUST NOT* access
directly the field _arr. To do changes, you can only use
the method swap_next(self, i).
NOTE: does *not* return anything!
NOTE: MUST execute in O(n^2), where n is the length of the array
"""
raise Exception("TODO IMPLEMENT ME !")
You can run tests only for swapsort with this command:
python3 -m unittest swap_array_test.SwapSortTest
Example usage:
[38]:
sar = SwapArray([8,4,2,4,2,7,3])
[39]:
swapsort(sar)
[40]:
print(sar)
SwapArray: [2, 2, 3, 4, 4, 7, 8]
Challenges
See Sorting challenges worksheet
[ ]: