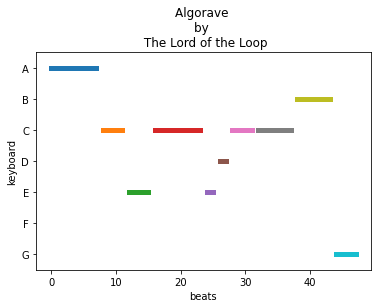Exam - Tue 12, Jul 2022
Scientific Programming - Data Science Master @ University of Trento
Download exercises and solutions
Part A - Music Sequencer
NOTICE: this part of the exam was ported to this page on softpython website
There you can find a more curated version (notice it may be longer than here)
Open Jupyter and start editing this notebook exam-2022-07-12.ipynb
ABC is a popular format to write music notation in plain text files, you can see an example by openining tunes1.abc with a text editor. A music sequencer is an editor software which typically displays notes as a matrix: you will parse simplified abc tunes and display their melodies in a matrix.
A1 parse_melody
Write a function which given a melody as a string of notes translates it to a list of tuples:
>>> parse_melody("|A4 C2 E2 |C4 E D C2 |C3 B3 G2 |")
[(0, 8), (2, 4), (4, 4), (2, 8), (4, 2), (3, 2), (2, 4), (2, 6), (1, 6), (6, 4)]
Each melody note is followed by its duration. If no duration number is specified, we assume it is one.
Each tuple first element represents a note as a number from 0 (A) to 6 (G) and the second element is the note length in the sequencer. We assume our sequencer has a resolution of two beats per note, so for us a note A would have length 2, a note A2 a length 4, a note A3 a length 6 and so on.
DO NOT care about spaces nor bars
|, they have no meaning at allUSE
ordpython function to get a character position
[2]:
def parse_melody(melody):
raise Exception('TODO IMPLEMENT ME !')
from pprint import pprint
melody1 = "|A4 C2 E2 |C4 E D C2 |C3 B3 G2 |"
pprint(parse_melody(melody1) )
assert parse_melody("||") == []
assert parse_melody("|A|") == [(0,2)]
assert parse_melody("|A3|") == [(0,6)]
assert parse_melody("|A B|") == [(0,2), (1,2)]
assert parse_melody("|C D|") == [(2,2), (3,2)]
assert parse_melody(" | G F | ") == [(6,2), (5,2)]
assert parse_melody("|D|B|") == [(3,2), (1,2)]
assert parse_melody("|D3 E4|") == [(3,6),(4,8)]
assert parse_melody("|F|A2 B|") == [(5,2),(0,4),(1,2)]
assert parse_melody("|A4 C2 E2 |C4 E D C2 |C3 B3 G2 |") == \
[(0, 8), (2, 4), (4, 4), (2, 8), (4, 2), (3, 2), (2, 4), (2, 6), (1, 6), (6, 4)]
A2 parse_tunes
An .abc file is a series of key:value fields. Keys are always one character long. Anything after a % is a comment and must be ignored
File tunes1.abc EXCERPT:
[3]:
with open("tunes1.abc", encoding='utf-8') as f: print(''.join(f.readlines()[0:18]))
%abc-2.1
H:Tune made in a dark algorithmic night % history and origin in header, so replicated in all tunes!
O:Trento
X:1 % index
T:Algorave % title
C:The Lord of the Loop % composer
M:4/4 % meter
K:C % key
|A4 C2 E2 |C4 E D C2 |C3 B3 G2 | % melodies can also have a comment
X:2
T:Transpose Your Head
C:Matrix Queen
O:Venice % overriding header
M:3/4
K:G
|F2 G4 |E4 E F|A2 B2 D2 |D3 E3 |C3 C3 |
First lines (3 in the example) are the file header, separated by tunes with a blank line.
first line must always be ignored
fields specified in the file header must be copied in all tunes.
Note a tune may override a field (es
O:Venice)
After the first blank line, there is the first tune:
Xis the tune index, convert it to integerMis the meter, convert it to a tuple of two integersKis the last field of metadatamelody line has no field key, it always follows line with
Kand it immediately begins with a pipe: convert it to list by callingparse_melody
Following tunes are separated by blank lines
Write a function parse_tunes which parses the file and outputs a list of dictionaries, one per tune. Use provided field_names to obtain dictionary keys. Full expected db is in expected_db1.py file.
DO NOT write hundreds of ifs
Special keys are listed above, all others should be treated in a generic way
DO NOT assume header always contains 'origin' and 'history'
It can contain any field, which has to be then copied in all the tunes, see tunes2.abc for extra examples.
Example (EXCERPT):
>>> tunes_db1 = parse_tunes('tunes1.abc')
>>> pprint(tunes_db1[:2],width=150)
[
{'composer': 'The Lord of the Loop',
'history': 'Tune made in a dark algorithmic night',
'index': 1,
'key': 'C',
'melody': [(0, 8), (2, 4), (4, 4), (2, 8), (4, 2), (3, 2), (2, 4), (2, 6), (1, 6), (6, 4)],
'meter': (4, 4),
'origin': 'Trento',
'title': 'Algorave'
},
{'composer': 'Matrix Queen',
'history': 'Tune made in a dark algorithmic night',
'index': 2,
'key': 'G',
'melody': [(5, 4),(6, 8),(4, 8),(4, 2),(5, 2),(0, 4),(1, 4),(3, 4),(3, 6),(4, 6),(2, 6),(2, 6)],
'meter': (3, 4),
'origin': 'Venice',
'title': 'Transpose Your Head'
}
]
[4]:
field_names = {
'C':'composer',
'D':'discography',
'H':'history',
'K':'key',
'M':'meter',
'O':'origin',
'T':'title',
'X':'index',
}
def parse_tunes(filename):
raise Exception('TODO IMPLEMENT ME !')
tunes_db1 = parse_tunes('tunes1.abc')
pprint(tunes_db1[:3],width=150)
[5]:
assert tunes_db1[0]['history']=='Tune made in a dark algorithmic night'
assert tunes_db1[0]['origin']=='Trento'
assert tunes_db1[0]['index']==1
assert tunes_db1[0]['title']=='Algorave'
assert tunes_db1[0]['composer']=='The Lord of the Loop'
assert tunes_db1[0]['meter']==(4,4)
assert tunes_db1[0]['key']== 'C'
assert tunes_db1[0]['melody']==\
[(0, 8), (2, 4), (4, 4), (2, 8), (4, 2), (3, 2), (2, 4), (2, 6), (1, 6), (6, 4)]
assert tunes_db1[1]['history']=='Tune made in a dark algorithmic night'
assert tunes_db1[1]['origin']=='Venice' # tests override
assert tunes_db1[1]['index']==2
assert tunes_db1[1]['title']=='Transpose Your Head'
assert tunes_db1[1]['composer']=='Matrix Queen'
assert tunes_db1[1]['meter']==(3,4)
assert tunes_db1[1]['key']== 'G'
assert tunes_db1[1]['melody']==\
[(5, 4), (6, 8), (4, 8), (4, 2), (5, 2), (0, 4), (1, 4), (3, 4), (3, 6), (4, 6), (2, 6), (2, 6)]
from expected_db1 import expected_db1
assert len(tunes_db1) == len(expected_db1)
assert tunes_db1 == expected_db1
tunes_db2 = parse_tunes('tunes2.abc')
pprint(tunes_db2)
from expected_db2 import expected_db2
assert tunes_db2 == expected_db2
[{'composer': 'Drum Shaman',
'discography': 'Sounds from the Jungle, 1968',
'history': 'Folk songs collected while travelling',
'index': 1,
'key': 'E',
'melody': [(6, 2),
(6, 4),
(6, 2),
(6, 2),
(0, 2),
(4, 4),
(4, 2),
(4, 2),
(3, 12)],
'meter': (4, 4),
'title': 'Jungle Beat'},
{'composer': 'The Crazy Gipsy',
'history': 'Folk songs collected while travelling',
'index': 2,
'key': 'G',
'melody': [(0, 6), (0, 6), (6, 4), (4, 6), (0, 6), (6, 4)],
'meter': (2, 4),
'title': 'Byte Polka'}]
A3 plot_tune
Write a function which takes a tune dictionary from the db and outputs a plot where the ys are all the notes on keyboard (we assume 7 notes without black keys) and xs represent the duration of a note. If you didn’t manage to implement it copy expected tune from expected_db1.py)
use beats as xs, remembering the shortest note has two beats
to increase thickness, use
linewidth=5parameter

[6]:
%matplotlib inline
import matplotlib.pyplot as plt
def plot_tune(tune):
raise Exception('TODO IMPLEMENT ME !')
plot_tune(tunes_db1[0])
Part B
Open Visual Studio Code and start editing the folder on your desktop
For running tests: open Accessories -> Terminal
B1.1 Theory
Write the solution in separate ``theory.txt`` file
Given a list L of \(n\) elements, please compute the asymptotic computational complexity of the myFun function, explaining your reasoning.
def myFun(L):
n = sum(L)
prods = {}
for i in range(len(L)):
prods[i] = 0
for j in range(len(L)):
prods[i] *= j
for k in range(len(L)//2):
prods[k] *= k
return prods
myFun([3, 9, 7, 5, 18, 19, 20])
B1.2 complexity
What do we mean when we say that an algorithm has asymptotic computational complexity \(O(n^3)\) ? What do we have to do to prove that an algorithm has asymptotic computational complexity \(O(n^3)\) ?
B2 BinTree same_rec
Open file bin_tree.py and implement this method:
def same_rec(self, other):
""" RETURN True if this binary tree is equal to other binary tree,
otherwise return False.
- MUST execute in O(n) where n is the number of nodes of the tree
- NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.SameRecTest
[9]:
from bin_tree_test import bt
t1 = bt(7,
bt(5))
t2 = bt(7,
bt(5))
t1.same_rec(t2)
[9]:
True
[10]:
t1 = bt(7,
None,
bt(9))
t2 = bt(7,
bt(11,
bt(7)))
t1.same_rec(t2)
[10]:
False
B3 GenericTree follow
Open file gen_tree.py and implement this method:
def follow(self, positions):
""" RETURN an array of node data, representing a branch from the
root down to a certain depth.
The path to follow is determined by given positions, which
is an array of integer indeces, see example.
- if provided indeces lead to non-existing nodes, raise ValueError
- IMPORTANT: *DO NOT* use recursion, use a couple of while instead.
- IMPORTANT: *DO NOT* attempt to convert siblings to
a python list !!!! Doing so will give you less points!
"""
Example:
level 01234
a
├b
├c
|└e
| ├f
| ├g
| |└i
| └h
└d
RETURNS
t.follow([]) [a] root data is always present
t.follow([0]) [a,b] b is the 0-th child of a
t.follow([2]) [a,d] d is the 2-nd child of a
t.follow([1,0,2]) [a,c,e,h] c is the 1-st child of a
e is the 0-th child of c
h is the 2-nd child of e
t.follow([1,0,1,0]) [a,c,e,g,i] c is the 1-st child of a
e is the 0-th child of c
g is the 1-st child of e
i is the 0-th child of g
Testing: python3 -m unittest gen_tree_test.FollowTest
[ ]: