Generic Trees

Download exercises zip 

(before editing read whole introduction sections 0.x)

0. Introduction

Before tackling generic trees please see first binary trees

What to do

unzip exercises in a folder, you should get something like this:

trees
   gen_tree.py
   gen_tree_sol.py
   gen_tree_test.py
   bin_tree_test.py
   bin_tree.py
   bin_tree_sol.py
   jupman.py
   sciprog.py
   trees.ipynb

open the editor of your choice (for example Visual Studio Code, Spyder or PyCharme), you will edit the files ending in .py files
Go on reading this notebook, and follow instuctions inside.

0.1 References

See

Luca Bianco Generic Tree theory
Trees on the book
- In particular, Vocabulary and definitions

labeled iiuiue9

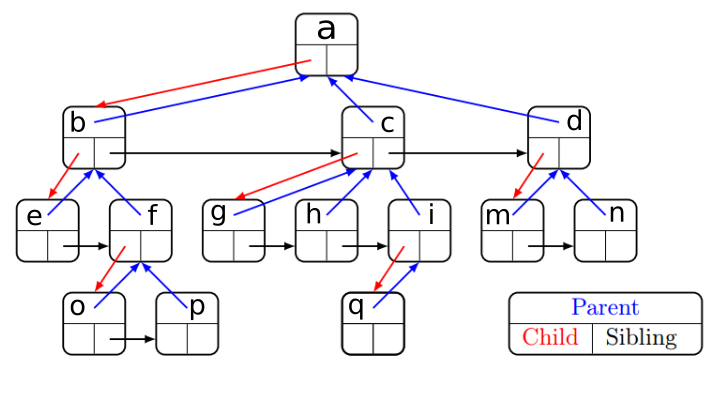
In this worksheet we are going to provide an implementation of a GenericTree class:

Why GenericTree ? Because many object hierarchies in real life tend to have many interlinked pointers this, in one form or another
Differently from the LinkedList, which actually had two classes Node and LinkedList that was pointing to the first node, in this case we just have one GenericTree class. So to grow a tree like the above one in the picture, for each of the boxes that you see we will need to create one instance of GenericTree and link it to the other instances.
Ordinary simple trees just hold pointers to the children. In this case, we have an enriched tree which holds ponters also up to the parent and on the right to the siblings. Whenever we are going to manipulate the tree, we need to take good care of updating these pointers.

Do we need sidelinks and backlinks ?:

Here we use sidelinks and backlinks like _sibling and _parent for exercise purposes, but keep in mind such extra links need to be properly managed when you write algorithms and thus increase the likelihood of introducing bugs.

As a general rule of thumb, if you are to design a data structure, always first try to start making it unidirectional (like for example the BinTree we’ve seen before). Then, if you notice you really need extra links (for example to quickly traverse a tree from a node up to the root), you can always add them in a later development iteration.

ROOT NODE: In this context, we call a node root if has no incoming edges and it has no parent nor sibling

DETACHING A NODE: In this context, when we detach a node from a tree, the node becomes the root of a new tree, which means it will have no link anymore with the tree it was in.

0.2 Code skeleton

Look at the files:

trees/gen_tree.py : the exercise to edit
trees/gen_tree_test.py: the tests to run. Do not modify this file.

Before starting to implement methods in GenericTree class, read all the following sub sections (starting with ‘0.x’)

0.3 Building trees

Let’s learn how to build GenericTree. For these trials, feel free to launch a Python 3 interpreter and load this module:

[2]:

from gen_tree_sol import *

0.3.1 Pointers

A GenericTree class holds 3 pointers that link it to the other nodes: _child, _sibling and _parent. So this time we have to manage more pointers, in particular beware of the _parent one which as a matter of fact creates cycles in the structure.

It also holds a value data which is provided by the user to store arbitrary data (could be ints, strings, lists, even other trees, we don’t care):

class GenericTree:

    def __init__(self, data):
        self._data = data
        self._child = None
        self._sibling = None
        self._parent = None

To create a tree of one node, just call the constructor passing whatever you want like this:

[3]:

tblah = GenericTree("blah")
tn = GenericTree(5)

Note that with the provided constructor you can’t pass children.

0.3.2 Building with `insert_child`

To grow a GenericTree, as basic building block you will have to implement insert_child:

def insert_child(self, new_child):
    """ Inserts new_child at the beginning of the children sequence. """

WARNING: here we insert a node !!

Differently from the BinTree, this time instead of passing data we pass a node. This can cause more troubles than before, as when we add a new_child we must be careful it doesn’t have wrong pointers. For example, think the case when you insert node B as child of node A, but by mistake you previously set B _child field to point to A. Such a cycle would not be a tree anymore and would basically disrupt any algorithm you would try to run.

You can call it like this:

[4]:

ta = GenericTree('a')
print(ta)   # 'a' is the root

[5]:

tb = GenericTree('b')
ta.insert_child(tb)
print(ta)

a
└b

a     'a' is the root
└b    'b' is the child . The '└' means just that it is also the last child of the siblings sequence

[6]:

tc = GenericTree('c')
ta.insert_child(tc)
print(ta)

a
├c
└b

a          # 'a' is the root
├c         # 'c' is inserted as the first child (would be shown on the left in the graph image)
└b         # 'b' is now the next sibling of c  The '\' means just that it
           #  is also the last child of the siblings sequence

[7]:

td = GenericTree('d')
tc.insert_child(td)
print(ta)

a
├c
│└d
└b

a         # 'a' is the root
├c        # 'c' is the first child of 'a'
|└d       # 'd' is the first child of 'c'
└b        # 'b' is the next sibling of c

0.3.3 Building with `gt`

If you need to test your data structure, we provide you with this handy function gt in gen_tree_test module that allows to easily construct trees from other trees.

WARNING: DO NOT USE gt inside your implementation code !!!! gt is just meant for testing.

def gt(*args):
    """ Shorthand function that returns a GenericTree containing the provided
        data and children. First parameter is the data, the following ones are the children.

[8]:

# first remember to import it from gen_tree_test:

from gen_tree_test import gt

# NOTE: this function is _not_ a class method, you can directly invoke it like this:
print(gt('a'))

[9]:

# NOTE: the external call gt('a', ......... )  INCLUDES gt('b') and gt('c') in the parameters !

print(gt('a', gt('b'), gt('c')))

a
├b
└c

0.4 Displaying trees side by side with `str_trees`

If you have a couple of trees, like the actual one you get from your method calls and the one you expect, it might be useful to display them side by side with the str_trees method in gen_tree_test module:

[10]:

# first remember to import it:

from gen_tree_test import str_trees

# NOTE: this function is _not_ a class method, you can directly invoke it like this:
print(str_trees(gt('a', gt('b')), gt('x', gt('y'), gt('z'))))

ACTUAL    EXPECTED
a         x
└b        ├y
          └z

0.5 Look at the tests

Have a look at the gen_tree_test.py file header, notice it imports GenericTree class from exercises file gen_tree:

from gen_tree import *
import unittest

0.6 Look at gen_tree_test.GenericTreeTest

Have a quick look at GenericTreeTest definitions inside gen_tree_test :

class GenericTreeTest(unittest.TestCase):

    def assertReturnNone(self, ret, function_name):
        """ Asserts method result ret equals None """

    def assertRoot(self, t):
        """ Checks provided node t is a root, if not raises AssertionError """

    def assertTreeEqual(self, t1, t2):
        """ Asserts the trees t1 and t2 are equal """

We see we added extra asserts you will later find used around in test methods. Of these ones, the most important is assertTreeEqual: when you have complex data structures like trees, it is helpful being able to compare the tree you obtain from your method calls to the tree you expect. This assertion we created provides a way to quickly display such differences.

1 Implement basic methods

labeled 99f9guggo

Start editing gen_tree.py, implementing methods in GenericTree in the order you find them in the next points.

IMPORTANT: All methods and functions without written inside raise Exception("TODO IMPLEMENT ME!") are already provided and you don’t need to edit them !

1.1 insert_child

Implement method insert_child, which is the basic building block for our GenericTree:

WARNING: here we insert a node !!

Differently from the BinTree, this time instead of passing data we pass a node. This implies that inside the insert_child method you will have to take care of pointers of new_child: for example, you will need to set the _parent pointer of new_child to point to the current node you are attaching to (that is, self)

def insert_child(self, new_child):
    """ Inserts new_child at the beginning of the children sequence. """

IMPORTANT: before proceding, make sure the tests for it pass by running:

python3 -m unittest gen_tree_test.InsertChildTest

QUESTION: Look at the tests, they are quite thourough and verbose. Why ?

1.2 insert_children

Implement insert_children:

def insert_children(self, new_children):
    """ Takes a list of children and inserts them at the beginning of the
        current children sequence,

        NOTE: in the new sequence new_children appear in the order they
              are passed to the function!


        For example:
            >>> t = gt('a', gt('b'), gt('c))
            >>> print t

            a
            ├b
            └c

            >>>  t.insert_children([gt('d'), gt('e')])
            >>> print t

            a
            ├d
            ├e
            ├b
            └c
    """

HINT 1: try to reuse insert_child, but note it inserts only to the left. Calling it on the input sequence you would get wrong ordering in the tree.

WARNING: Function description does not say anything about changing the input new_children, so users calling your method don’t expect you to modify it ! However, you can internally produce a new Python list out of the input one, if you wish to.

Testing: python3 -m unittest gen_tree_test.InsertChildrenTest

1.3 insert_sibling

Implement insert_sibling:

def insert_sibling(self, new_sibling):
    """ Inserts new_sibling as the *immediate* next sibling.

        If self is a root, raises a ValueError.
    """

Testing: python3 -m unittest tree_test.InsertSiblingTest

Examples:

[12]:

tb = gt('b')
ta = gt('a', tb, gt('c'))
print(ta)

a
├b
└c

[13]:

tx = gt('x', gt('y'))
print(tx)

x
└y

[14]:

tb.insert_sibling(tx)
print(ta)

a
├b
├x
│└y
└c

QUESTION: if you call insert_sibling an a root node such as ta, you should get a ValueError. Why? Does it make sense to have parentless brothers ?

ta.insert_sibling(g('z'))

---------------------------------------------------------------------------
Exception                                 Traceback (most recent call last)
<ipython-input-35-a1e4ba8b1ee5> in <module>()
----> 1 ta.insert_sibling(gt('z'))

~/Da/prj/sciprolab2/prj/trees/tree_sol.py in insert_sibling(self, new_sibling)
    128         """
    129         if (self.is_root()):
--> 130             raise ValueError("Can't add siblings to a root node !!")
    131
    132         new_sibling._parent = self._parent

Exception: Can't add siblings to a root node !!

1.4 `insert_siblings`

Testing: python3 -m unittest gen_tree_test.InsertSiblingsTest

1.5 `detach_child`

QUESTION: does a detached child have still any parent or sibling ?

Testing: python3 -m unittest gen_tree_test.DetachChildTest

1.6 `detach_sibling`

Testing: python3 -m unittest gen_tree_test.DetachSiblingTest

1.7 `detach`

Testing: python3 -m unittest gen_tree_test.DetachTest

1.8 `ancestors`

labeled iu9ug8g9

Implement ancestors:

def ancestors(self):
        """ Return the ancestors up until the root as a Python list.
            First item in the list will be the parent of this node.

            NOTE: this function return the *nodes*, not the data.
        """

Testing: python3 -m unittest gen_tree_test.AncestorsTest

Examples:

ancestors of p: f, b, a
ancestors of h: c, a
ancestors of a: empty list

2 Implement more complex functions

After you understood well and implemented the previous methods, you can continue with the following ones:

2.1 `grandchildren`

Implement the grandchildren method. NOTE: it returns the data inside the nodes, NOT the nodes !!!!!

def grandchildren(self):
    """ Returns a python list containing the data of all the
        grandchildren of this node.

        - Data must be from left to right order in the tree horizontal
          representation (or up to down in the vertical representation).
        - If there are no grandchildren, returns an empty array.

        For example, for this tree:

        a
        ├b
        │├c
        │└d
        │ └g
        ├e
        └f
         └h

        Returns ['c','d','h']
    """

Testing: python3 -m unittest gen_tree_test.ZagTest

Examples:

[15]:

ta = gt('a', gt('b', gt('c')))
print(ta)

a
└b
 └c

[16]:

print(ta.grandchildren())

['c']

[17]:

ta = gt('a', gt('b'))
print(ta)

a
└b

[18]:

print(ta.grandchildren())

[]

[19]:

ta = gt('a', gt('b', gt('c'), gt('d')), gt('e', gt('f')) )
print(ta)

a
├b
│├c
│└d
└e
 └f

[20]:

print(ta.grandchildren())

['c', 'd', 'f']

2.2 Zig Zag

Here you will be visiting a generic tree in various ways.

labeled jii4u43

2.2.1 zig

The method zig must return as output a list of data of the root and all the nodes in the chain of child attributes. Basically, you just have to follow the red lines and gather data in a list, until there are no more red lines to follow.

Testing: python3 -m unittest tree_test.ZigTest

Examples: in the labeled tree in the image, these would be the results of calling zig on various nodes:

From a: ['a','b', 'e']
From b: ['b', 'e']
From c: ['c', 'g']
From h: ['h']
From q: ['h']

2.2.2 zag

This function is quite similar to zig, but this time it gathers data going right, along the sibling arrows.

Testing: python3 -m unittest gen_tree_test.ZagTest

Examples: in the labeled tree in the image, these would be the results of calling zag on various nodes:

From a : ['a']
From b : ['b', 'c', 'd']
From o : ['o', 'p']

2.2.3 zigzag

As you are surely thinking, zig and zag alone are boring. So let’s mix the concepts, and go zigzaging. This time you will write a function zigzag, that first zigs collecting data along the child vertical red chain as much as it can. Then, if the last node links to at least a sibling, the method continues to collect data along the siblings horizontal chain as much as it can. At this point, if it finds a child, it goes zigging again along the child vertical red chain as much as it can, and then horizontal zaging, and so on. It continues zig-zaging like this until it reaches a node that has no child nor sibling: when this happens returns the list of data found so far.

Testing: python3 -m unittest tree_test.ZigZagTest

Examples: in the labeled tree in the image, these would be the results of calling zigzag on various nodes:

From a: ['a', 'b', 'e', 'f', 'o']
From c: ['c', 'g', 'h', 'i', 'q'] NOTE: if node h had a child z, the process would still proceed to i
From d: ['d', 'm', 'n']
From o: ['o', 'p']
From n: ['n']

2.3 uncles

Implement the uncles method:

def uncles(self):
    """ RETURN a python list containing the data of all the uncles
        of this node (that is, *all* the siblings of its parent).

        NOTE: returns also the father siblings which are *BEFORE*
              the father !!

        - Data must be from left to right order in the tree horizontal
          representation (or up to down in the vertical representation)
        - If there are no uncles, returns an empty array.

        For example, for this tree:

        a
        ├b
        │├c
        │└d
        │ └g
        ├e
        │└h
        └f

        calling this method on 'h' returns ['b','f']
    """

Testing: python3 -m unittest gen_tree_test.UnclesTest

Example usages:

[21]:

td = gt('d')
tb = gt('b')
ta = gt('a', tb,  gt('c', td), gt('e'))
print(ta)

a
├b
├c
│└d
└e

[22]:

print(td.uncles())

['b', 'e']

[23]:

print(tb.uncles())

[]

2.4 common_ancestor

labeled iiug9f9

Implement the method common_ancestor:

def common_ancestor(self, gt2):
    """ RETURN the first common ancestor of current node and the provided
        gt2 node

        - If gt2 is not a node of the same tree, raises LookupError

        NOTE: this function returns a *node*, not the data.

        Ideally, this method should perform in O(h) where h is the height
        of the tree.

        HINT: you should use a Python Set). If you can't figure out how
              to make it that fast, try to make it at worst O(h^2)

    """

Testing: python3 -m unittest gen_tree_test.CommonAncestorTest

Examples:

common ancestor of g and i: tree rooted at c
common_ancestor of g and q: tree rooted at c
common_ancestor of e and d: tree rooted at a

2.5 mirror

def mirror(self):
    """ Modifies this tree by mirroring it, that is, reverses the order
        of all children of this node and of all its descendants

        - MUST work in O(n) where n is the number of nodes
        - MUST change the order of nodes, NOT the data (so don't touch the
               data !)
        - DON'T create new nodes
        - It is acceptable to use a recursive method.


        Example:

        a     <-    Becomes:    a
        ├b                      ├i
        │├c                     ├e
        │└d                     │├h
        ├e                      │├g
        │├f                     │└f
        │├g                     └b
        │└h                      ├d
        └i                       └c

    """

Testing: python3 -m unittest gen_tree_test.MirrorTest

2.6 clone

Implement the method clone:

def clone(self):
    """ Clones this tree, by returning an *entirely* new tree which is an
        exact copy of this tree (so returned node and *all* its descendants
        must be new).

        - MUST run in O(n) where n is the number of nodes
        - a recursive method is acceptable.
    """

Testing: python3 -m unittest gen_tree_test.CloneTest

2.7 rightmost

labeled i99kfdf

In the example above, the rightmost branch of a is given by the node sequence a,d,n

Implement this method:

def rightmost(self):
        """ RETURN a list containing the *data* of the nodes
            in the *rightmost* branch of the tree.

            Example:

            a
            ├b
            ├c
            |└e
            └d
             ├f
             └g
              ├h
              └i

            should give

            ['a','d','g','i']
        """

Testing: python3 -m unittest gen_tree_test.RightmostTest

2.8 fill_left

Implement fill_left method:

def fill_left(self, stuff):
    """ MODIFIES the tree by filling the leftmost branch data
        with values from provided array 'stuff'

        - if there aren't enough nodes to fill, raise ValueError
        - root data is not modified
        - *DO NOT* use recursion

    """

Testing: python3 -m unittest gen_tree_test.FillLeftTest

Example:

[24]:

from gen_tree_test import gt
from gen_tree_sol import *

[25]:

t  = gt('a',
            gt('b',
                    gt('e',
                            gt('f'),
                            gt('g',
                                    gt('i')),
                    gt('h')),
            gt('c'),
            gt('d')))

[26]:

print(t)

a
└b
 ├e
 │├f
 │├g
 ││└i
 │└h
 ├c
 └d

[27]:

t.fill_left(['x','y'])

[28]:

print(t)

a
└x
 ├y
 │├f
 │├g
 ││└i
 │└h
 ├c
 └d

[29]:

t.fill_left(['W','V','T'])
print(t)

a
└W
 ├V
 │├T
 │├g
 ││└i
 │└h
 ├c
 └d

2.9 follow

Implement this method:

def follow(self, positions):
    """ RETURN an array of node data, representing a branch from the
        root down to a certain depth.
        The path to follow is determined by given positions, which
        is an array of integer indeces, see example.

        - if provided indeces lead to non-existing nodes, raise ValueError
        - IMPORTANT: *DO NOT* use recursion, use a couple of while instead.
        - IMPORTANT: *DO NOT* attempt to convert siblings to
                     a python list !!!! Doing so will give you less points!
    """

Example:

              level  01234

                     a
                     ├b
                     ├c
                     |└e
                     | ├f
                     | ├g
                     | |└i
                     | └h
                     └d

                    RETURNS
t.follow([])        [a]          root data is always present
t.follow([0])       [a,b]        b is the 0-th child of a
t.follow([2])       [a,d]        d is the 2-nd child of a
t.follow([1,0,2])   [a,c,e,h]    c is the 1-st child of a
                                 e is the 0-th child of c
                                 h is the 2-nd child of e
t.follow([1,0,1,0]) [a,c,e,g,i]  c is the 1-st child of a
                                 e is the 0-th child of c
                                 g is the 1-st child of e
                                 i is the 0-th child of g

Testing: python3 -m unittest gen_tree_test.FollowTest

2.10 is_triangle

A triangle is a node which has exactly two children.

Let’s see some example:

      a
    /   \
   /     \
  b ----- c
 /|\     /
d-e-f   g
       / \
      h---i
         /
        l

The tree above can also be represented like this:

a
├b
│├d
│├e
│└f
└c
 └g
  ├h
  └i
   └l

node a is a triangle because has exactly two children b and c, note it doesn’t matter if b or c have children)
b is not a triangle (has 3 children)
c and i are not triangles (have only 1 child)
g is a triangle as it has exactly two children h and i
d, e, f, h and l are not triangles, because they have zero children

Now implement this method:

def is_triangle(self, elems):
    """ RETURN True if this node is a triangle matching the data
        given by list elems.

        In order to match:
        - first list item must be equal to this node data
        - second list item must be equal to this node first child data
        - third list item must be equal to this node second child data

        - if elems has less than three elements, raises ValueError
    """

Testing: python -m unittest gen_tree_test.IsTriangleTest

Examples:

[31]:

from gen_tree_test import gt

[32]:

# this is the tree from the example above

tb = gt('b', gt('d'), gt('e'), gt('f'))
tg = gt('g', gt('h'), gt('i', gt('l')))
ta = gt('a', tb, gt('c', tg))

ta.is_triangle(['a','b','c'])

[32]:

True

[33]:

ta.is_triangle(['b','c','a'])

[33]:

False

[34]:

tb.is_triangle(['b','d','e'])

[34]:

False

[35]:

tg.is_triangle(['g','h','i'])

[35]:

True

[36]:

tg.is_triangle(['g','i','h'])

[36]:

False

2.11 has_triangle

Implement this method:

def has_triangle(self, elems):
    """ RETURN True if this node *or one of its descendants* is a triangle
        matching given elems. Otherwise, return False.

        - a recursive solution is acceptable
    """

Testing: python -m unittest gen_tree_test.HasTriangleTest

Examples:

[37]:

# example tree seen at the beginning

tb = gt('b', gt('d'), gt('e'), gt('f'))
tg = gt('g', gt('h'), gt('i', gt('l')))
tc = gt('c', tg)
ta = gt('a', tb, tc)

ta.has_triangle(['a','b','c'])

[37]:

True

[38]:

ta.has_triangle(['a','c','b'])

[38]:

False

[39]:

ta.has_triangle(['b','c','a'])

[39]:

False

[40]:

tb.is_triangle(['b','d','e'])

[40]:

False

[41]:

tg.has_triangle(['g','h','i'])

[41]:

True

[42]:

tc.has_triangle(['g','h','i'])  # check recursion

[42]:

True

[43]:

ta.has_triangle(['g','h','i'])  # check recursion

[43]:

True

2.12 marvelous

Edit this method:

def marvelous(self):
    """ MODIFIES each node data replacing it with the concatenation
        of its leaves data

        - MUST USE a recursive solution
        - assume node data is always a string
    """

Testing: python3 -m unittest generic_tree_test.MarvelousTest

Example: NOTE: leaves may be any character! Here we show them as uppercase but they might also be lowercase.

[45]:

from gen_tree_sol import *
from gen_tree_test import gt

t = gt('a',
          gt('b',
                gt('M'),
                gt('A'),
                gt('R')),
          gt('c',
                gt('e',
                      gt('V'),),
                gt('E')),
          gt('d',
                gt('L'),
                gt('f',
                      gt('O'),
                      gt('U'),),
                gt('S')))

[46]:

print(t)

a
├b
│├M
│├A
│└R
├c
│├e
││└V
│└E
└d
 ├L
 ├f
 │├O
 │└U
 └S

[47]:

t.marvelous()
print(t)

MARVELOUS
├MAR
│├M
│├A
│└R
├VE
│├V
││└V
│└E
└LOUS
 ├L
 ├OU
 │├O
 │└U
 └S

[ ]:

Generic Trees

Download exercises zip

0. Introduction

What to do

0.1 References

0.2 Code skeleton

0.3 Building trees

0.3.1 Pointers

0.3.2 Building with insert_child

0.3.3 Building with gt

0.4 Displaying trees side by side with str_trees

0.5 Look at the tests

0.6 Look at gen_tree_test.GenericTreeTest

1 Implement basic methods

1.1 insert_child

1.2 insert_children

1.3 insert_sibling

1.4 insert_siblings

1.5 detach_child

1.6 detach_sibling

1.7 detach

1.8 ancestors

2 Implement more complex functions

2.1 grandchildren

2.2 Zig Zag

2.2.1 zig

2.2.2 zag

2.2.3 zigzag

2.3 uncles

2.4 common_ancestor

2.5 mirror

2.6 clone

2.7 rightmost

2.8 fill_left

2.9 follow

2.10 is_triangle

2.11 has_triangle

2.12 marvelous

Download exercises zip 

0.3.2 Building with `insert_child`

0.3.3 Building with `gt`

0.4 Displaying trees side by side with `str_trees`

1.4 `insert_siblings`

1.5 `detach_child`

1.6 `detach_sibling`

1.7 `detach`

1.8 `ancestors`

2.1 `grandchildren`