CircularQueue
Download exercises zip
A circular queue is a data structure which when initialized occupies a fixed amount of memory called capacity.
1. Introduction
Typically, fixed size data structures are found in systems programming (i.e. programming drivers), when space is constrained and you want predictable results as much as possible. For us, it will be an example of modular arithmetic usage. In our implementation, to store data we will use a Python list, which we initialize with a number of empty cells equal to capacity. During initialization, it does’t matter what we actually put inside cells, in this case we will use None. Note that
capacity never changes, and cells are never added nor removed from the list. What varies during execution is the actual content of the cells, the index pointing to the head of the queue (from which elements are dequeued) and another number we call size which is a number telling us how many elements are present in the queue. Summing head and size numbers will allow us to determine where to enqueue elements at the tail of the queue - to avoid overflow, we will have to take modulus of
the sum. Keep reading for details.
To implement the circular queue you can use this pseudo code:

QUESTION: Pseudo code is meant to give a general overview of the algorithms, and can often leave out implementation details, such as defining what to do when things don’t work as expected. If you were to implement this in a real life scenario, do you see any particular problem or adaptation we could do to improve it?
QUESTION: If we can insert any kind of object in the queue including None, are we going to have troubles with definitions like top() above?
In our implementation, we will:
use more pythonic names, with underscores instead of camelcase.
explicitly handle exceptions and corner cases
be able to insert any kind of object in the queue
Initial queue will be populated with
Noneobjects, and will have length set to provided capacity_sizeis the current dimension of the queue, which is different from the initial providedcapacity.we consider
capacityas fixed: it will never change during execution. For this reason, since we use a Python list to represent the data, we don’t need an extra variable to hold it, just getting the list length will suffice._headis an index pointing to the next element to be dequeuedelements are inserted at the position pointed to by
(_head + _size) % capacity(), and dequeued from position pointed by_head. The module%operator allows using a list as it were circular, that is, if an index apparently falls outside the list, with the modulus it gets transformed to a small index. Since_sizecan never exceedcapacity(), the formula(_head + _size) % capacity()never points to a place which could overwrite elements not yet dequeued, except cases when the queue has_size==0or_size==capacity()which are to be treated as special.enqueuing and dequeing operations don’t modify list length !
2. Example
[2]:
from circular_queue_sol import CircularQueue
At the beginning, we declare the capacity 7, filling an array of seven cells with None values:
[3]:
q = CircularQueue(7)
[4]:
from sciprog import draw_circular_queue
draw_circular_queue(q)

Note that tail pointer always points to the next available cell where a new enqueued item will be placed. For now, you can ignore the % capacity operator, just focus on the head + size part:
[5]:
q.enqueue('a')
[6]:
draw_circular_queue(q)

As expected, we see that tail now points to index 1, the next place where we will enqueue new arrivals:
[7]:
q.enqueue('b')
draw_circular_queue(q)
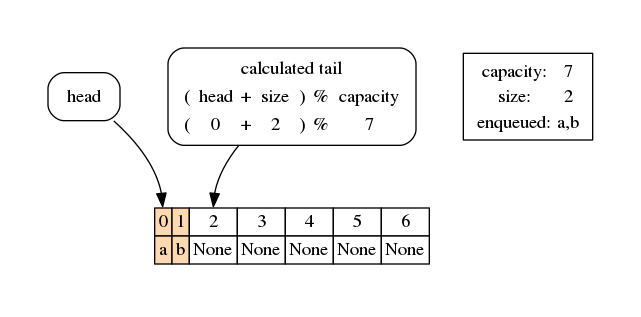
[8]:
q.enqueue('c')
q.enqueue('d')
q.enqueue('e')
draw_circular_queue(q)

Let’s say we want to dequeue one guy: dequeuing always happens at the head pointer:
[9]:
q.dequeue()
[9]:
'a'
[10]:
draw_circular_queue(q)
Notice how the dequeue method returned the item 'a', so to make it available to whoever calls the method, yet 'a' is still present inside the array and head index was moved forward. The reason is that once the head is moved, we won’t care anymore about cells outside the enqueued elements span, so there is no need to waste a writing operation to overwrite the 'a' with a None.
[11]:
q.dequeue()
[11]:
'b'
[12]:
draw_circular_queue(q)

Let’s try now to enqueue more stuff:
[13]:
q.enqueue('f')
[14]:
draw_circular_queue(q)

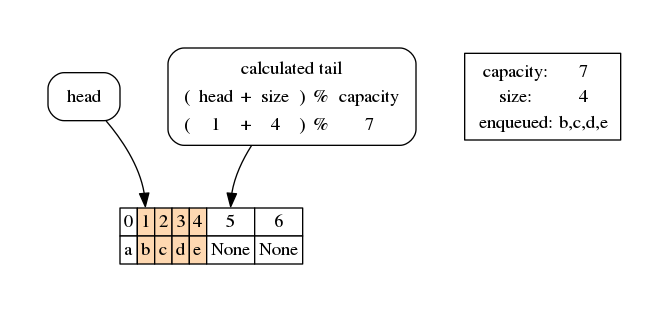
Now we reached a critical position, and we must decide what happens when we enqueue again. Since the tail is supposed to always point to the next available cell for enqueuing, as soon as we enqueue an item here the last cell will be filled and we will need to move the tail… somewhere. If you remember, we said that the items outside the span between the head and the tail are considered as removed from the queue and can be safely overwritten. So we can set the tail to the other side of the
array, at zero index (hence the circular queue). Now, how to obtain index 0 ? We could use some if command, but it turns out math already provides us with a handy operator called modulo, which in Python is represented by the percentage % operator. The modulo gives us the remainder of the division of two numbers: in this case, what is the reminder of 2 + 4 + 1 divided by 7? Exactly the 0 we were looking for:
[15]:
q.enqueue('g')
[16]:
draw_circular_queue(q)
Let’s try to enqueue another item:
[17]:
q.enqueue('h')
[18]:
draw_circular_queue(q)

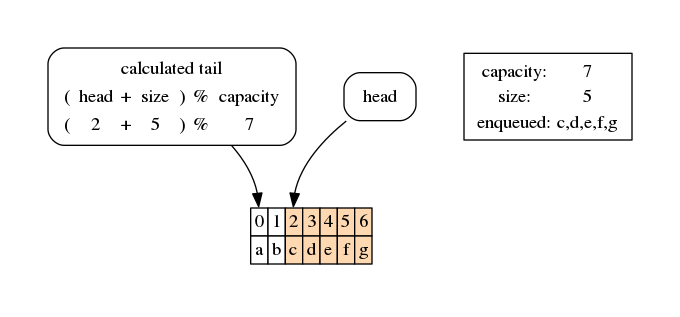
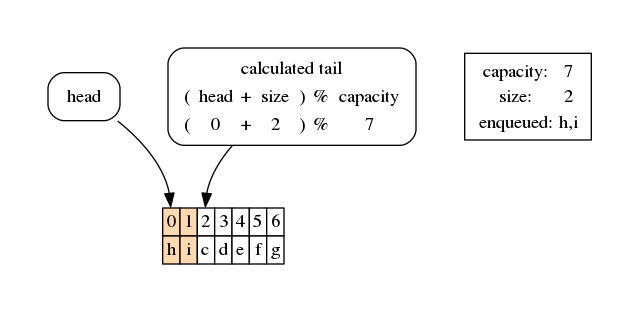
As predicted, a was overwritten and the tail is now the reminder of the division between 2 + 5 + 1 and 7, that is 1, the index right after the last cell we filled in.
If we now enqueue another item, we reach another extremal situation:
[19]:
q.enqueue('i')
[20]:
draw_circular_queue(q)
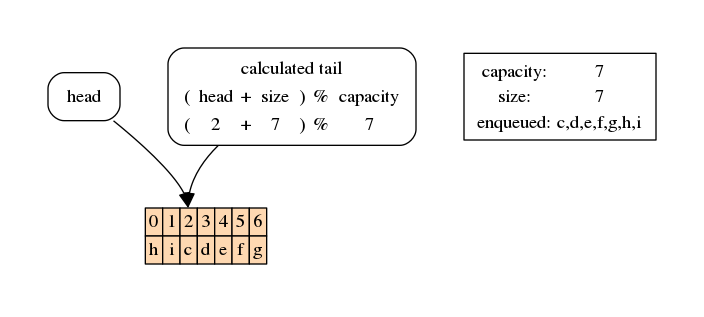
Now the calculated tail is pointing at the head - exactly as when the queue was empty, but now we now the queue instead is full because the size equals the capacity. In this situation, if we try to enqueue more stuff we should get an error:
[21]:
try:
q.enqueue('z')
except Exception as ex:
print(ex)
Queue is full !
[22]:
q.dequeue()
[22]:
'c'
[23]:
draw_circular_queue(q)

[24]:
q.dequeue()
[24]:
'd'
[25]:
draw_circular_queue(q)

Let’s dequeue more stuff until we reach this other extraml situation:
[26]:
print(q.dequeue())
print(q.dequeue())
e
f
[27]:
draw_circular_queue(q)

Now dequeuing will move the head to the right. We could use an if to detect we are at the right bound and set the head to the leftmost index 0 but math again helps us with the modulo operator:
\(head = (head + 1) \;\%\; capacity\)
With this formula we have:
\(head = (6 + 1) \;\% \;7\)
which is exactly \(0\)
[28]:
q.dequeue()
[28]:
'g'
[29]:
draw_circular_queue(q)
[30]:
q.dequeue()
[30]:
'h'
[31]:
draw_circular_queue(q)

[32]:
q.dequeue()
[32]:
'i'
[33]:
draw_circular_queue(q)

We now have another singular condition, with head equal to tail and size zero. A further attempt at dequeuing should now give us an error:
[34]:
try:
q.dequeue()
except Exception as ex:
print(ex)
Queue is empty !
3. Circular span
First try to get an understanding of modulo operator and variables involved by implementing this (simple?) function (it’s completely separate from CircularQueue class):
Show solution[35]:
def in_span(i, head, size, capacity):
""" Return True if index i is included in the circular span
between head (INCLUDED) index and calculated tail index (EXCLUDED)
Otherwise, return False.
"""
raise Exception('TODO IMPLEMENT ME !')
"""
t
h
0123456
abcdefg
"""
assert in_span(0, 0, 0, 7) == False
assert in_span(1, 0, 0, 7) == False
assert in_span(2, 0, 0, 7) == False
"""
ht
0123456
abcdefg
"""
assert in_span(0, 0, 1, 7) == True
assert in_span(1, 0, 1, 7) == False
assert in_span(2, 0, 1, 7) == False
"""
h-t
0123456
abcdefg
"""
assert in_span(0, 0, 2, 7) == True
assert in_span(1, 0, 2, 7) == True
assert in_span(2, 0, 2, 7) == False
"""
h--t
0123456
abcdefg
"""
assert in_span(0, 2, 3, 7) == False
assert in_span(1, 2, 3, 7) == False
assert in_span(2, 2, 3, 7) == True
assert in_span(3, 2, 3, 7) == True
assert in_span(4, 2, 3, 7) == True
assert in_span(5, 2, 3, 7) == False
assert in_span(6, 2, 3, 7) == False
"""
h---t
0123456
abcdefg
"""
assert in_span(0, 2, 4, 7) == False
assert in_span(1, 2, 4, 7) == False
assert in_span(2, 2, 4, 7) == True
assert in_span(3, 2, 4, 7) == True
assert in_span(4, 2, 4, 7) == True
assert in_span(5, 2, 4, 7) == True
assert in_span(6, 2, 4, 7) == False
"""
-t h---
0123456
abcdefg
"""
assert in_span(0, 3, 5, 7) == True
assert in_span(1, 3, 5, 7) == False
assert in_span(2, 3, 5, 7) == False
assert in_span(3, 3, 5, 7) == True
assert in_span(4, 3, 5, 7) == True
assert in_span(5, 3, 5, 7) == True
assert in_span(6, 3, 5, 7) == True
"""
--t h-
0123456
abcdefg
"""
assert in_span(0, 5, 4, 7) == True
assert in_span(1, 5, 4, 7) == True
assert in_span(2, 5, 4, 7) == False
assert in_span(3, 5, 4, 7) == False
assert in_span(4, 5, 4, 7) == False
assert in_span(5, 5, 4, 7) == True
assert in_span(6, 5, 4, 7) == True
"""
t
--h----
0123456
abcdefg
"""
assert in_span(2, 2, 7, 7) == True
4. Implement CircularQueue
Implement methods in file circular_queue.py in the order they are presented, and test them with circular_queue_test.py
python3 -m unittest circular_queue_test