Midterm - Thu 10, Jan 2019

Scientific Programming - Data Science Master @ University of Trento

Download exercises and solution

What to do

1. Download sciprog-ds-2019-01-10-exam.zip and extract it on your desktop. Folder content should be like this:

sciprog-ds-2019-01-10-FIRSTNAME-LASTNAME-ID
    gaps.py
    gaps_test.py
    tasks.py
    tasks_test.py
    exits.py
    exits_test.py
    jupman.py
    sciprog.py

2. Rename sciprog-ds-2019-01-10-FIRSTNAME-LASTNAME-ID folder: put your name, lastname an id number, like sciprog-ds-2019-01-10-john-doe-432432

From now on, you will be editing the files in that folder. At the end of the exam, that is what will be evaluated.

3. Edit the files following the instructions in this worksheet for each exercise. Every exercise should take max 25 mins. If it takes longer, leave it and try another exercise.

4. When done:

if you have unitn login: zip and send to examina.icts.unitn.it

If you don’t have unitn login: tell instructors and we will download your work manually

Introduction

B1 Theory

Please write the solution in the text file theory.txt

Given the following function:

def fun(N, M):
    S1 = set(N)
    S2 = set(M)
    res = []
    for x in S1:
        if x in S2:
            for i in range(N.count(x)):
                res.append(x)
    return res

let N and M be two lists of length n and m, respectively. What is the computational complexity of function fun() with respect to n and m?

B2 Gaps linked list

Given a linked list of size n which only contains integers, a gap is an index i, 0<i<n, such that L[i−1]<L[i]. For the purpose of this exercise, we assume an empy list or a list with one element have zero gaps

Example:

 data:  9 7 6 8 9 2 2 5
index:  0 1 2 3 4 5 6 7

contains three gaps [3,4,7] because:

• number 8 at index 3 is greater than previous number 6 at index 2

• number 9 at index 4 is greater than previous number 8 at index 3

• number 5 at index 7 is greater than previous number 2 at index 6

Open file gaps.py and implement this method:

def gaps(self):
    """ Assuming all the data in the linked list is made by numbers,
        finds the gaps in the LinkedList and return them as a Python list.

        - we assume empty list and list of one element have zero gaps
        - MUST perform in O(n) where n is the length of the list

        NOTE: gaps to return are *indeces* , *not* data!!!!
    """

Testing: python3 -m unittest gaps_test.GapsTest

B3 Tasks stack

Very often, you begin to do a task just to discover it requires doing 3 other tasks, so you start carrying them out one at a time and discover one of them actually requires to do yet another two other subtasks….

To represent the fact a task may have subtasks, we will use a dictionary mapping a task label to a list of subtasks, each represented as a label. For example:

subtasks = {
        'a':['b','g'],
        'b':['c','d','e'],
        'c':['f'],
        'd':['g'],
        'e':[],
        'f':[],
        'g':[]
    }

Task a requires subtasks b andg to be carried out (in this order), but task b requires subtasks c, d and e to be done. c requires f to be done, and d requires g.

You will have to implement a function called do and use a Stack data structure, which is already provided and you don’t need to implement. Let’s see an example of execution.

IMPORTANT: In the execution example, there are many prints just to help you understand what’s going on, but the only thing we actually care about is the final list returned by the function!

IMPORTANT: notice subtasks are scheduled in reversed order, so the item on top of the stack will be the first to get executed !

from tasks_sol import *

do('a', subtasks)

DEBUG:  Stack:   elements=['a']
DEBUG:  Doing task a, scheduling subtasks ['b', 'g']
DEBUG:           Stack:   elements=['g', 'b']
DEBUG:  Doing task b, scheduling subtasks ['c', 'd', 'e']
DEBUG:           Stack:   elements=['g', 'e', 'd', 'c']
DEBUG:  Doing task c, scheduling subtasks ['f']
DEBUG:           Stack:   elements=['g', 'e', 'd', 'f']
DEBUG:  Doing task f, scheduling subtasks []
DEBUG:           Nothing else to do!
DEBUG:           Stack:   elements=['g', 'e', 'd']
DEBUG:  Doing task d, scheduling subtasks ['g']
DEBUG:           Stack:   elements=['g', 'e', 'g']
DEBUG:  Doing task g, scheduling subtasks []
DEBUG:           Nothing else to do!
DEBUG:           Stack:   elements=['g', 'e']
DEBUG:  Doing task e, scheduling subtasks []
DEBUG:           Nothing else to do!
DEBUG:           Stack:   elements=['g']
DEBUG:  Doing task g, scheduling subtasks []
DEBUG:           Nothing else to do!
DEBUG:           Stack:   elements=[]

['a', 'b', 'c', 'f', 'd', 'g', 'e', 'g']

The Stack you must use is simple and supports push, pop, and is_empty operations:

s = Stack()

print(s)

Stack:   elements=[]

s.is_empty()

True

s.push('a')

print(s)

Stack:   elements=['a']

s.push('b')

print(s)

Stack:   elements=['a', 'b']

s.pop()

'b'

print(s)

Stack:   elements=['a']

B3.1 do

Now open tasks_stack.py and implement function do:

def do(task, subtasks):
    """ Takes a task to perform and a dictionary of subtasks,
        and RETURN a list of performed tasks

        - To implement it, inside create a Stack instance and a while cycle.
        - DO *NOT* use a recursive function
        - Inside the function, you can use a print like "I'm doing task a',
          but that is only to help yourself in debugging, only the
          list returned by the function will be considered in the evaluation!
    """

Testing: python3 -m unittest tasks_test.DoTest

B3.2 do_level

In this exercise, you are asked to implement a slightly more complex version of the previous function where on the Stack you push two-valued tuples, containing the task label and the associated level. The first task has level 0, the immediate subtask has level 1, the subtask of the subtask has level 2 and so on and so forth. In the list returned by the function, you will put such tuples.

One possibile use is to display the executed tasks as an indented tree, where the indentation is determined by the level. Here we see an example:

IMPORTANT: Again, the prints are only to let you understand what’s going on, and you are not required to code them. The only thing that really matters is the list the function must return !

subtasks = {
        'a':['b','g'],
        'b':['c','d','e'],
        'c':['f'],
        'd':['g'],
        'e':[],
        'f':[],
        'g':[]
    }

do_level('a', subtasks)

DEBUG:                                                  Stack:   elements=[('a', 0)]
DEBUG:  I'm doing   a               level=0 Stack:   elements=[('g', 1), ('b', 1)]
DEBUG:  I'm doing     b             level=1 Stack:   elements=[('g', 1), ('e', 2), ('d', 2), ('c', 2)]
DEBUG:  I'm doing       c           level=2 Stack:   elements=[('g', 1), ('e', 2), ('d', 2), ('f', 3)]
DEBUG:  I'm doing         f         level=3 Stack:   elements=[('g', 1), ('e', 2), ('d', 2)]
DEBUG:  I'm doing       d           level=2 Stack:   elements=[('g', 1), ('e', 2), ('g', 3)]
DEBUG:  I'm doing         g         level=3 Stack:   elements=[('g', 1), ('e', 2)]
DEBUG:  I'm doing       e           level=2 Stack:   elements=[('g', 1)]
DEBUG:  I'm doing     g             level=1 Stack:   elements=[]

[('a', 0),
 ('b', 1),
 ('c', 2),
 ('f', 3),
 ('d', 2),
 ('g', 3),
 ('e', 2),
 ('g', 1)]

Now implement the function:

def do_level(task, subtasks):
    """ Takes a task to perform and a dictionary of subtasks,
        and RETURN a list of performed tasks, as tuples (task label, level)

        - To implement it, use a Stack and a while cycle
        - DO *NOT* use a recursive function
        - Inside the function, you can use a print like "I'm doing task a',
          but that is only to help yourself in debugging, only the
          list returned by the function will be considered in the evaluation
    """

Testing: python3 -m unittest tasks_test.DoLevelTest

B4 Exits graph

There is a place nearby Trento called Silent Hill, where people always study and do little else. Unfortunately, one day an unethical biotech AI experiment goes wrong and a buggy cyborg is left free to roam in the building. To avoid panic, you are quickly asked to devise an evacuation plan. The place is a well known labyrinth, with endless corridors also looping into cycles. But you know you can model this network as a digraph, and decide to represent crossings as nodes. When a crossing has a door to leave the building, its label starts with letter e, while when there is no such door the label starts with letter n.

In the example below, there are three exits e1, e2, and e3. Given a node, say n1, you want to tell the crowd in that node the shortest paths leading to the three exits. To avoid congestion, one third of the crowd may be told to go to e2, one third to reach e1 and the remaining third will go to e3 even if they are farther than e2.

In python terms, we would like to obtain a dictionary of paths like the following, where as keys we have the exits and as values the shortest sequence of nodes from n1 leading to that exit

{
    'e1': ['n1', 'n2', 'e1'],
    'e2': ['n1', 'e2'],
    'e3': ['n1', 'e2', 'n3', 'e3']
}

from sciprog import draw_dig
from exits_sol import *
from exits_test import dig

G = dig({'n1':['n2','e2'],
         'n2':['e1'],
         'e1':['n1'],
         'e2':['n2','n3', 'n4'],
         'n3':['e3'],
         'n4':['n1']})
draw_dig(G)

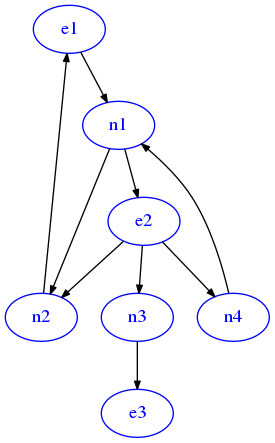
You will solve the exercise in steps, so open exits_sol.py and proceed reading the following points.

B4.1 cp

Implement this method

def cp(self, source):
    """ Performs a BFS search starting from provided node label source and
        RETURN a dictionary of nodes representing the visit tree in the
        child-to-parent format, that is, each key is a node label and as value
        has the node label from which it was discovered for the first time

        So if node "n2" was discovered for the first time while
        inspecting the neighbors of "n1", then in the output dictionary there
        will be the pair "n2":"n1".

        The source node will have None as parent, so if source is "n1" in the
        output dictionary there will be the pair  "n1": None

        NOTE: This method must *NOT* distinguish between exits
              and normal nodes, in the tests we label them n1, e1 etc just
              because we will reuse in next exercise
        NOTE: You are allowed to put debug prints, but the only thing that
              matters for the evaluation and tests to pass is the returned
              dictionary
    """

Testing: python3 -m unittest exits_test.CpTest

Example:

G.cp('n1')

DEBUG:  Removed from queue: n1
DEBUG:    Found neighbor: n2
DEBUG:      not yet visited, enqueueing ..
DEBUG:    Found neighbor: e2
DEBUG:      not yet visited, enqueueing ..
DEBUG:    Queue is: ['n2', 'e2']
DEBUG:  Removed from queue: n2
DEBUG:    Found neighbor: e1
DEBUG:      not yet visited, enqueueing ..
DEBUG:    Queue is: ['e2', 'e1']
DEBUG:  Removed from queue: e2
DEBUG:    Found neighbor: n2
DEBUG:      already visited
DEBUG:    Found neighbor: n3
DEBUG:      not yet visited, enqueueing ..
DEBUG:    Found neighbor: n4
DEBUG:      not yet visited, enqueueing ..
DEBUG:    Queue is: ['e1', 'n3', 'n4']
DEBUG:  Removed from queue: e1
DEBUG:    Found neighbor: n1
DEBUG:      already visited
DEBUG:    Queue is: ['n3', 'n4']
DEBUG:  Removed from queue: n3
DEBUG:    Found neighbor: e3
DEBUG:      not yet visited, enqueueing ..
DEBUG:    Queue is: ['n4', 'e3']
DEBUG:  Removed from queue: n4
DEBUG:    Found neighbor: n1
DEBUG:      already visited
DEBUG:    Queue is: ['e3']
DEBUG:  Removed from queue: e3
DEBUG:    Queue is: []

{'n1': None,
 'n2': 'n1',
 'e2': 'n1',
 'e1': 'n2',
 'n3': 'e2',
 'n4': 'e2',
 'e3': 'n3'}

Basically, the dictionary above represents this visit tree:

   n1
  /   \
n2     e2
 \    /  \
 e1   n3  n4
      |
      e3

B4.2 exits

Implement this function. NOTE: the function is external to class DiGraph.

def exits(cp):
    """
        INPUT: a dictionary of nodes representing a visit tree in the
        child-to-parent format, that is, each key is a node label and as value
        has its parent as a node label. The root has associated None as parent.

        OUTPUT: a dictionary mapping node labels of exits to the shortest path
                from the root to the exit (root and exit included)

    """

Testing: python3 -m unittest exits_test.ExitsTest

Example:

# as example we can use the same dictionary outputted by the cp call in the previous exercise

visit_cp = { 'e1': 'n2',
             'e2': 'n1',
             'e3': 'n3',
             'n1': None,
             'n2': 'n1',
             'n3': 'e2',
             'n4': 'e2'
            }
exits(visit_cp)

{'e1': ['n1', 'n2', 'e1'], 'e2': ['n1', 'e2'], 'e3': ['n1', 'e2', 'n3', 'e3']}