Midterm B- Thu 16, Dec 2021
Scientific Programming - Data Science Master @ University of Trento
Download exercises and solutions
B1 Theory
Write the solution in separate ``theory.txt`` file
B1.1 complexity
Given a list \(L\) of \(n\) elements, please compute the asymptotic computational complexity of the my_fun function, explaining your reasoning.
[2]:
def my_fun2(L):
n = len(L)
tmp = []
for i in range(n):
for j in range(n):
tmp.append(L[i]/(L[j]))
return tmp
def my_fun(L):
n = len(L)
if n <= 1:
return 1
else:
L1 = L[0:n//3]
L2 = L[2*(n//3):]
a = my_fun(L1) + max(my_fun2(L1))
b = my_fun(L2) + max(my_fun2(L2))
return a - b
B1.2 postfix
Postfix notation is used by compilers to process expressions efficiently, respecting operator precedence without needing to scan the whole expression multiple times (programming languages let us write expressions using the infix notation for simplicity). Think of a function implementing the evaluation of expressions in postfix notation. Which data structure would you use, and why? Explain your reasoning.
Infix notation: a op1 b (e.g. 7 * 4)
Postfix notation: a b op1 (e.g. 7 4 *)
Infix notation: a op1 b op2 c op3 d (e.g. 7 + 4 * 5 + 9)
Postfix notation: a b c op1 op2 d op3 (e.g. 7 4 5 * + 9 +)
B2 norep
Open Visual Studio Code and start editing the folder on your desktop
For running tests: open Accessories -> Terminal
Open file linked_list.py and implement the method norep:
def norep(self):
""" MODIFIES this list by removing all the consecutive
repetitions from it.
- MUST perform in O(n), where n is the list size.
"""
Testing: python3 -m unittest more_test.NorepTest
Example:
[3]:
from linked_list_sol import *
[4]:
ll = LinkedList()
ll.add('e')
ll.add('c')
ll.add('c')
ll.add('c')
ll.add('d')
ll.add('d')
ll.add('b')
ll.add('a')
ll.add('a')
ll.add('c')
ll.add('c')
ll.add('a')
ll.add('a')
ll.add('a')
[5]:
print(ll)
LinkedList: a,a,a,c,c,a,a,b,d,d,c,c,c,e
[6]:
ll.norep()
[7]:
print(ll)
LinkedList: a,c,a,b,d,c,e
B3 family_sum_rec
Open bin_tree.py and implement this method:
def family_sum_rec(self):
""" MODIFIES the tree by adding to each node data its *original* parent and children data
- MUST execute in O(n) where n is the size of the tree
- a recursive implementation is acceptable
- HINT: you will probably want to define a helper function
"""
Testing: python3 -m unittest bin_tree_test.FamilySumRec
Example:
[8]:
from bin_tree_test import bt
[9]:
t = bt(5,
bt(1,
bt(4,
None,
bt(3)),
bt(2)),
bt(9,
bt(11)))
[10]:
from sciprog import draw_bt
draw_bt(t)
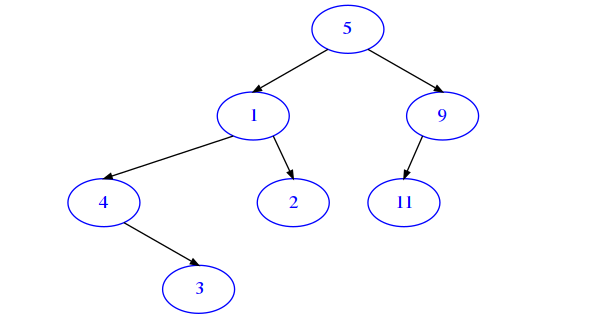
[11]:
t.family_sum_rec()
[12]:
draw_bt(t)

You need to sum to each node data its original parent data + original left child data + original right child data , for example:
Root: 15 = 5 + 0 + 1 + 9
left child of root: 12 = 1 + 5 + 4 + 2
right child of root: 25 = 9 + 5 + 11 + 0
leftmost grandchild of root: 8 = 4 + 1 + 0 + 3