Exam - Fri 11, Jun 2021

Scientific Programming - Data Science Master @ University of Trento

Download exercises and solutions

Part A - Trans-Atlantic Slave Trade

NOTICE: this part of the exam was ported to softpython website

There you can find a more curated version (notice it may be longer than here)

Open Jupyter and start editing this notebook exam-2021-06-11.ipynb

Two centuries ago the shipping of enslaved Africans across the Atlantic was morally indistinguishable from shipping sugar or textiles. This migration experience covers an era of very dramatic shifts in perceptions of good and evil, which provided the Americas with a crucial labor force for their own economic development.

Data provider: The Trans-Atlantic Slave Trade Database. 2020. SlaveVoyages. https://www.slavevoyages.org. You are enouraged to explore the dataset with the very interesting online tool they built, in particular check out the Maps and Timelapse tabs.

Data license:

• Historical data: The Trans-Atlantic Slave Trade Database. 2020. SlaveVoyages. https://www.slavevoyages.org (accessed June 9, 2020). License: Public domain (use restrictions do not apply).

• Imputed data: Estimates. 2020. SlaveVoyages. https://slavevoyages.org/assessment/estimates (accessed June 9, 2020). License: Creative Commons Attribution-Noncommercial 3.0 United States License.

A1 read_trade

Each line in slave-trade.csv represents a ship voyage from a purchase place to a landing place. Parse it with a csv reader and output a list of dictionaries, one per voyage according to the output excerpt.

• Each ship has a nation flag NATINIMP

• Each voyage has purchase place code MJBYPTIMP and a landing place code MJSLPTIMP with five digits format xyzvt that indicate a specific town: you MUST save more generic codes of the form xyz00 which indicate broader regions.

• WARNING 1: convert to int only VOYAGEID and YEARAM, leave MJBYPTIMP and MJSLPTIMP as strings

• WARNING 2: some codes in slave-trade.csv have a space instead of a number, in those cases save code 00000

import pandas as pd
import numpy as np
df = pd.read_csv('slave-trade.csv', encoding='UTF-8')
df[df.VOYAGEID.isin([1, 2024, 2393, 4190])]

	VOYAGEID	YEARAM	NATINIMP	MJBYPTIMP	MJSLPTIMP
0	1	1817	Portugal/Brazil	60820	50299
2000	2024	1840	U.S.A.	60615	31399
2361	2393	1829	Spain/Uruguay	60212
4000	4190	1854	U.S.A.	60515	31301

Region labels: For each location you need to also save its label, which you can find in separate file region-codes.csv (load the file with a csv reader)

• WARNING 1: in region-codes.csv there are only codes in format xyz00

• WARNING 2: some region codes are missing, in those cases place label 'unknown'

import pandas as pd
dfr = pd.read_csv('region-codes.csv', encoding='UTF-8', dtype=str)
dfr[dfr.Value.isin(['60800','60600','31300','50200','60500'])]

	Value	Region
47	31300	Cuba
84	50200	Bahia
92	60500	Bight of Benin
93	60600	Bight of Biafra and Gulf of Guinea islands
95	60800	Southeast Africa and Indian Ocean islands

Show solution

import csv

def read_voyages(slave_trade_csv, region_codes_csv):


    with open(region_codes_csv, encoding='utf-8', newline='') as fregions:
        my_reader = csv.DictReader(fregions, delimiter=',')

        regions_db = {}
        for d in my_reader:
            regions_db[d['Value']] = d['Region']

    with open(slave_trade_csv, encoding='utf-8', newline='') as f:
        my_reader = csv.DictReader(f, delimiter=',')

        ret = []

        for d in my_reader:

            voyage = {}
            voyage['id'] = int(d['VOYAGEID'])
            voyage['year'] = int(d['YEARAM'])
            voyage['flag'] = d['NATINIMP']

            if  d['MJBYPTIMP'].strip():
                pur_reg = d['MJBYPTIMP'][:3] + '00'
                voyage['purchase_id'] = pur_reg
                if pur_reg in regions_db:
                    voyage['purchase_label'] = regions_db[pur_reg]
                else:
                    voyage['purchase_label'] = 'unknown'
            else:
                voyage['purchase_id'] = '00000'
                voyage['purchase_label'] = 'unknown'

            if d['MJSLPTIMP'].strip():
                lan_reg = d['MJSLPTIMP'][:3] + '00'
                voyage['landing_id'] = lan_reg
                if lan_reg in regions_db:
                    voyage['landing_label'] = regions_db[lan_reg]
                else:
                    voyage['landing_label'] = 'unknown'
            else:
                voyage['landing_id'] = '00000'
                voyage['landing_label'] = 'unknown'

            ret.append(voyage)

        return ret


voyages_db = read_voyages('slave-trade.csv', 'region-codes.csv')

print('OUTPUT EXCERPT:')
from pprint import pformat
print('[\n' +',\n'.join([pformat(voyages_db[vid]) for vid in [0,2000,2361, 4000]]) + ',\n  .\n  .\n]')

OUTPUT EXCERPT:
[
{'flag': 'Portugal/Brazil',
 'id': 1,
 'landing_id': '50200',
 'landing_label': 'Bahia',
 'purchase_id': '60800',
 'purchase_label': 'Southeast Africa and Indian Ocean islands',
 'year': 1817},
{'flag': 'U.S.A.',
 'id': 2024,
 'landing_id': '31300',
 'landing_label': 'Cuba',
 'purchase_id': '60600',
 'purchase_label': 'Bight of Biafra and Gulf of Guinea islands',
 'year': 1840},
{'flag': 'Spain/Uruguay',
 'id': 2393,
 'landing_id': '00000',
 'landing_label': 'unknown',
 'purchase_id': '60200',
 'purchase_label': 'Sierra Leone',
 'year': 1829},
{'flag': 'U.S.A.',
 'id': 4190,
 'landing_id': '31300',
 'landing_label': 'Cuba',
 'purchase_id': '60500',
 'purchase_label': 'Bight of Benin',
 'year': 1854},
  .
  .
]

import csv

def read_voyages(slave_trade_csv, region_codes_csv):
    raise Exception('TODO IMPLEMENT ME !')

voyages_db = read_voyages('slave-trade.csv', 'region-codes.csv')

print('OUTPUT EXCERPT:')
from pprint import pformat
print('[\n' +',\n'.join([pformat(voyages_db[vid]) for vid in [0,2000,2361, 4000]]) + ',\n  .\n  .\n]')

OUTPUT EXCERPT:
[
{'flag': 'Portugal/Brazil',
 'id': 1,
 'landing_id': '50200',
 'landing_label': 'Bahia',
 'purchase_id': '60800',
 'purchase_label': 'Southeast Africa and Indian Ocean islands',
 'year': 1817},
{'flag': 'U.S.A.',
 'id': 2024,
 'landing_id': '31300',
 'landing_label': 'Cuba',
 'purchase_id': '60600',
 'purchase_label': 'Bight of Biafra and Gulf of Guinea islands',
 'year': 1840},
{'flag': 'Spain/Uruguay',
 'id': 2393,
 'landing_id': '00000',
 'landing_label': 'unknown',
 'purchase_id': '60200',
 'purchase_label': 'Sierra Leone',
 'year': 1829},
{'flag': 'U.S.A.',
 'id': 4190,
 'landing_id': '31300',
 'landing_label': 'Cuba',
 'purchase_id': '60500',
 'purchase_label': 'Bight of Benin',
 'year': 1854},
  .
  .
]

# TESTING
from pprint import pformat; from expected_db import expected_db
for i in range(0, len(expected_db)):
    if expected_db[i] != voyages_db[i]:
        print('\nERROR at index', i, ':')
        print('  ACTUAL:\n', pformat(voyages_db[i]))
        print('  EXPECTED:\n', pformat(expected_db[i]))
        break

A2 Deportation

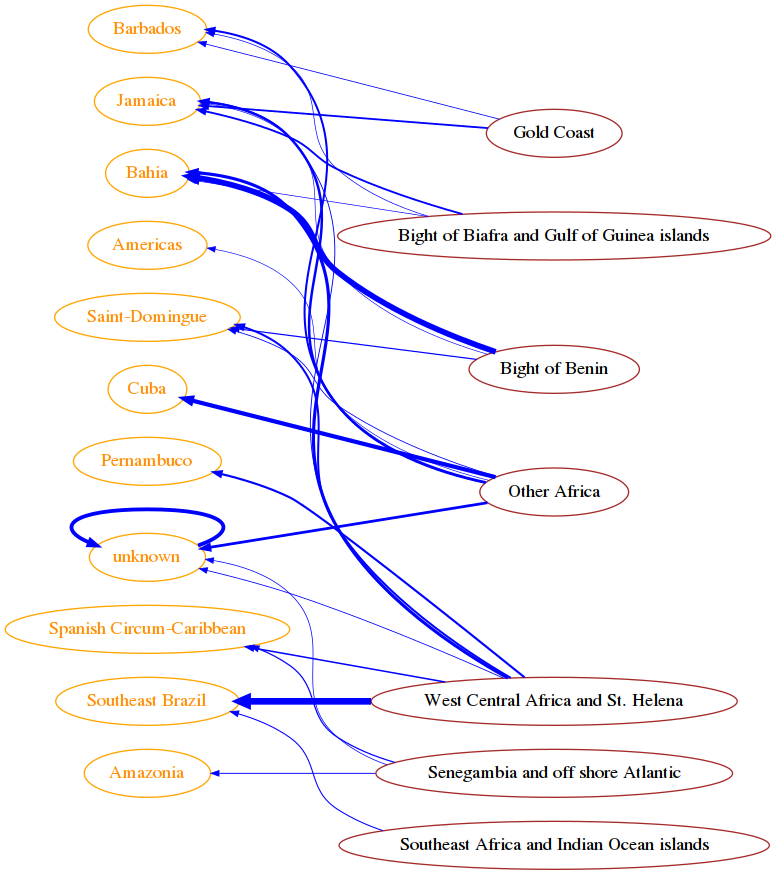
For each link purchase -> landing place, count in how many voyages it was present, then draw result in networkx.

• as edge weight use a normalized value from 0.0 to 1.0 (maximal count found in the graph)

• show only edges with weight greater or equal to min_weight

• to display the graph from right to left, set G.graph['graph']= {'rankdir':'RL'}

• for networkx attributes see this example

Show solution

import networkx as nx
from sciprog import draw_nx

def show_deportation(voyages, min_weight):


    edges = {}

    for v in voyages_db:
        t = (v['purchase_id'], v['landing_id'])
        if t in edges:
            edges[t] += 1
        else:
            edges[t] = 1



    G = nx.DiGraph()
    G.graph['graph']= {'rankdir':'RL'}    # force horiz right to left layout

    mx = max(edges.values())
    for v in voyages_db:
        s = edges[(v['purchase_id'], v['landing_id'])]
        r = s / mx
        if r >= min_weight:
            G.add_node(v['purchase_id'], fontcolor='black', color='brown', label=v['purchase_label'])
            G.add_node(v['landing_id'], fontcolor='darkorange', color='orange', label=v['landing_label'])
            G.add_edge(v['purchase_id'],v['landing_id'],
                       color="blue",
                       penwidth= 5 * r,
                       weight=r)

    draw_nx(G)

show_deportation(voyages_db, 0.09)
#show_deportation(voyages_db, 0.06)

COUNTS EXCERPT SOLUTION:
{
  ('60800', '50200') : 48,
  ('60700', '50200') : 1301,
  ('60700', '50400') : 2770,
  ('60800', '50400') : 443,
  ('60900', '50400') : 196,
    .
    .
}

import networkx as nx
from sciprog import draw_nx

def show_deportation(voyages, min_weight):
    raise Exception('TODO IMPLEMENT ME !')
show_deportation(voyages_db, 0.09)
#show_deportation(voyages_db, 0.06)

COUNTS EXCERPT SOLUTION:
{
  ('60800', '50200') : 48,
  ('60700', '50200') : 1301,
  ('60700', '50400') : 2770,
  ('60800', '50400') : 443,
  ('60900', '50400') : 196,
    .
    .
}

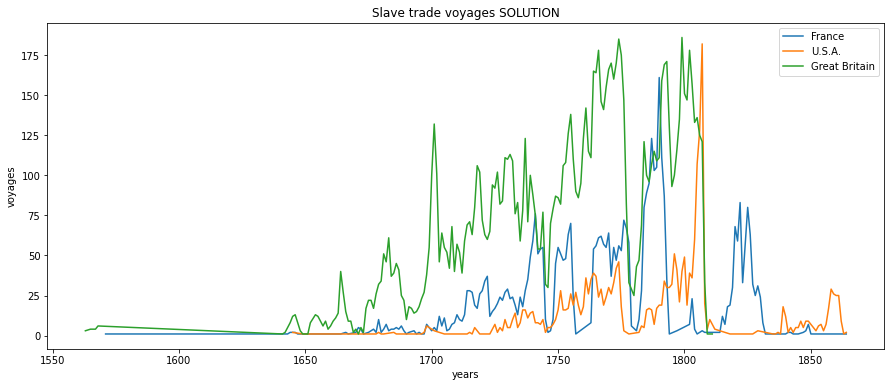
A3 The time to stop

Given a nation flag, plot inside draw_time the number of voyages per year done by ships belonging to that flag.

DO NOT call plt.show nor plt.figure

• we show some counts example but to calculate the data feel free to use any method you want

• to associate a plot to a label, use i.e. plt.plot(xs, ys, label='France')

Show solution

%matplotlib inline
import matplotlib.pyplot as plt

def draw_time(voyages, flag):


    plt.title("Slave trade voyages SOLUTION")
    plt.xlabel('years')
    plt.ylabel('voyages')

    counts = {}
    for v in voyages:
        if v['flag'] == flag:
            y = v['year']
            if y in counts:
                counts[y] += 1
            else:
                counts[y] = 1



    xs = sorted(counts.keys())
    ys = [counts[x] for x in xs]
    plt.plot(xs, ys, label=flag)


fig = plt.figure(figsize=(15,6))
draw_time(voyages_db, 'France')
draw_time(voyages_db, 'U.S.A.')
draw_time(voyages_db, 'Great Britain')
plt.legend()
plt.show()

France COUNTS EXCERPT SOLUTION:
{
        1816:7,
       1819:30,
       1821:59,
       .
       .
              }
U.S.A. COUNTS EXCERPT SOLUTION:
{
        1821:1,
        1827:1,
        1837:2,
       .
       .
              }
Great Britain COUNTS EXCERPT SOLUTION:
{
        1810:1,
        1809:1,
        1811:1,
       .
       .
              }

%matplotlib inline
import matplotlib.pyplot as plt

def draw_time(voyages, flag):
    raise Exception('TODO IMPLEMENT ME !')

fig = plt.figure(figsize=(15,6))
draw_time(voyages_db, 'France')
draw_time(voyages_db, 'U.S.A.')
draw_time(voyages_db, 'Great Britain')
plt.legend()
plt.show()

France COUNTS EXCERPT SOLUTION:
{
        1816:7,
       1819:30,
       1821:59,
       .
       .
              }
U.S.A. COUNTS EXCERPT SOLUTION:
{
        1821:1,
        1827:1,
        1837:2,
       .
       .
              }
Great Britain COUNTS EXCERPT SOLUTION:
{
        1810:1,
        1809:1,
        1811:1,
       .
       .
              }

Part B

• Open Visual Studio Code and start editing the folder on your desktop

B1 Theory

Write the solution in separate ``theory.txt`` file

B1.1 Complexity

Given a list L of \(n\) elements, please compute the asymptotic computational complexity of the following function, explaining your reasoning.

def my_fun(L):
    T = []
    N = len(L)
    for i in range(N//2):
        k = 0
        tmp = 0
        while k < 4:
            tmp += L[i]*k
            k = k + 1
        T.insert(0,tmp)

    return T

B1.2 Graph

What is a depth first search (DFS) of a graph? Please answer briefly and then provide a possible DFS (illustrating the reasoning behind the answer) of the following graph starting from the node a

B2 - is_heap_stack

Open bin_tree.py and implement:

def is_heap_stack(self):
    """ A tree is a min heap if each node data is less or equal than its children data.
        RETURN True if the tree is a min heap, False otherwise

        - DO *NOT* use recursion
        - implement it with a while and a stack (as a python list)
        - MUST run in O(n), where n is the tree size
    """

Testing: python3 -m unittest bin_tree_test

from bin_tree_test import bt
from bin_tree_sol import *
t = bt(7,
        bt(9,
                bt(10,
                        bt(40)),
                bt(14)),
        bt(20,
                None,
                bt(30,
                        bt(50),
                        bt(90))))

t.is_heap_stack()

True

t = bt(7,
        bt(9,
                bt(10,
                        bt(40)),
                bt(14)),
        bt(20,
                None,
                bt(30,
                        bt(11),
                        bt(90))))
t.is_heap_stack()

False

B3 - sepel

Open linked_list and implement this method:

def sepel(self, el):
    """ Separates this list into two lists:

        - this list will have all nodes without el as data
        - the other list will contain all nodes with el as data

        - IMPORTANT: DO *NOT* create new nodes, REUSE existing ones!!
        - MUST execute in O(n), where n is the length of the list
    """

Testing: python3 -m unittest linked_list_test

Example:

from linked_list_sol import *
la = LinkedList()
la.add('c')
la.add('e')
la.add('c')
la.add('d')
la.add('c')
la.add('c')
la.add('b')
la.add('a')
la.add('c')

print(la)

LinkedList: c,a,b,c,c,d,c,e,c

lb = la.sepel('c')

print(la)

LinkedList: a,b,d,e

print(lb)

LinkedList: c,c,c,c,c