Binary Trees
Download exercises zip
(before editing read whole introduction section)
Here we only deal with binary trees, for generic trees see separate notebook.
What to do
unzip exercises in a folder, you should get something like this:
trees
bin_tree_test.py
bin_tree.py
bin_tree_sol.py
gen_tree_test.py
gen_tree.py
gen_tree_sol.py
jupman.py
sciprog.py
bin-trees.ipynb
gen-trees.ipynb
open the editor of your choice (for example Visual Studio Code, Spyder or PyCharme), you will edit the files ending in
.pyfilesGo on reading this notebook, and follow instuctions inside.
0. Introduction
0.1 References
See
Luca Bianco theory here
-
In particular, Vocabulary and definitions
0.2 Terminology - relations

0.3 Terminology - levels

0.4 Terminology - shapes

In this worksheet we are first going to provide an implementation of a BinTree class:
Differently from the
LinkedList, which actually had two classesNodeandLinkedListthat was pointing to the first node, in this case we just have oneBinTreeclass.Each
BinTreeinstance may have a leftBinTreeinstance and may have a rightBinTreeinstance, while absence of a branch is marked withNone. This reflects the recursive nature of trees.To grow a tree, first you need to create an instance of
BinTree, and then you call.insert_leftor.insert_rightmethods on it and pass data. Keep reading to see how to do it.
0.2 Code skeleton
Look at the files:
trees/bin_tree.py: the exercise to edittrees/bin_tree_test.py: the tests to run. Do not modify this file.
Before starting to implement methods in BinTree class, read all the following sub sections (starting with ‘0.x’)
0.3 Building trees
Let’s learn how to build BinTree. For these trials, feel free to launch a Python 3 interpreter and load this module:
[2]:
from bin_tree_sol import *
0.3.1 Pointers
A BinTree class holds 2 pointers that link it to other nodes: _left, and _right
It also holds a value data which is provided by the user to store arbitrary data (could be ints, strings, lists, even other trees, we don’t care):
class BinTree:
def __init__(self, data):
self._data = data
self._left = None
self._right = None
NOTE: BinTree as defined here is unidirectional, that is, has no backlinks (so no _parent field).
Formally, a tree as described in discrete mathematics books is always unidirectional (can’t have any cycle) and every node can have at most one incoming link. When we program, though, for convenience we may decide to have or not have backlinks (later with GenericTree we will see an example)
To create a BinTree of one node, just call the constructor passing whatever you want like this:
[3]:
tblah = BinTree("blah")
tn = BinTree(5)
Note that with the provided constructor you can’t pass children.
0.3.2 Building with insert_left
To grow a BinTree, as basic building block you will have to implement insert_left:
def insert_left(self, data):
""" Takes as input DATA (*NOT* a node !!) and MODIFIES current
node this way:
- First creates a new BinTree (let's call it B) into which
provided data is wrapped.
- Then:
- if there is no left node in self, new node B is attached to
the left of self
- if there already is a left node L, it is substituted by
new node B, and L becomes the left node of B
"""
You can call it like this:
[4]:
t = BinTree('a')
t.insert_left('c')
[5]:
print(t)
a
├c
└
[6]:
t.insert_left('b')
[7]:
print(t)
a
├b
│├c
│└
└
[8]:
t.left().data()
[8]:
'b'
[9]:
t.left().left().data()
[9]:
'c'
0.3.3 Building with bt
If you need to test your data structure, we provide you with this handy function bt in bin_tree_test module that allows to easily construct trees from other trees.
WARNING: DO NOT USE bt inside your implementation code !!!! bt is just meant for testing.
def bt(*args):
""" Shorthand function that returns a GenericTree containing the provided
data and children. First parameter is the data, the following ones are the children.
[10]:
from bin_tree_test import bt
bt('a')
print(bt('a'))
a
[11]:
print(bt('a', None, bt('b')))
a
├
└b
[12]:
print(bt('a', bt('b'), bt('c')))
a
├b
└c
[13]:
print(bt('a', bt('b'), bt('c', bt('d'), None)) )
a
├b
└c
├d
└
1. Insertions
1.1 insert_left
Implement insert_left
def insert_left(self, data):
""" Takes as input DATA (*NOT* a node !!) and MODIFIES current node
this way:
- First creates a new BinTree (let's call it B) into which
provided data is wrapped.
- Then:
- if there is no left node in self, new node B is attached to
the left of self
- if there already is a left node L, it is substituted by
new node B, and L becomes the left node of B
Testing: python3 -m unittest bin_tree_test.InsertLeftTest
1.2 insert_right
def insert_right(self, data):
""" Takes as input DATA (*NOT* a node !!) and MODIFIES current node
this way:
- First creates a new BinTree (let's call it B) into which
provided data is wrapped.
- Then:
- if there is no right node in self, new node B is attached
to the right of self
- if there already is a right node L, it is substituted by
new node B, and L becomes the right node of B
"""
Testing: python3 -m unittest bin_tree_test.InsertRightTest
2. Recursive visit
In these exercises, we are going to implement methods which do recursive calls. Before doing it, we should ask oursevles why. Tyipically, recursive calls are present in funcitonal languages. Is Python one of them? Python is a general purpose language, that allows writing imperative, object-oriented code and also sports some, but not all functional programming features. Unfortunately, one notably missing feature is the capability to efficiently perform recursive calls. If too many recursive calls happen, you will probabily get a ‘Recursion limit exceed’ error. So why should we bother?
It turns out that recursive code is much shorter and elegant than corrisponding imperative one (which would often use stacks). So to gain a first understanding of problems, it might be beneficial to think about a recursive solution. After that, we may increase efficiency by explicitly using a stack instead of recursive calls.
When devising recursive algorithms on binary trees, given a parent node P (in the methods it would be self) a good strategy to start with is to consider all possible cases you can have:
No child |
Left child |
Right child |
Both children |
|---|---|---|---|
|
|
|
|
Let’s see an application of the idea.
2.1 sum_rec
Supposing all nodes hold a number, let’s see how to write a method that returns the sum of all numbers in the tree. We can define sum recursively:
if a node has no children: the sum is equal to the node data
if a node has only left child: the sum is equal to the node data plus the (recursive) sum of left child
if a node has only right child: the sum is equal to the node data plus the (recursive) sum of right child
if a node has both left and right child: the sum is equal to the node data plus the (recursive) sum of left child and the (recursive) sum of the right child
Example: black numbers are node data, purple numbers are the respective sums.
Let’s look at node with black number 10: its sum is 23, which is given by its data 10, plus 1 ( the recursive sum of the left child 1), plus 12 ( recursive sum of the right child 7)

def sum_rec(self):
""" Supposing the tree holds integer numbers in all nodes,
RETURN the sum of the numbers.
- implement it as a recursive Depth First Search (DFS) traversal
NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.ContainsRecTest
Code example:
[15]:
t = bt(3,
bt(10,
bt(1),
bt(7,
bt(5))),
bt(9,
bt(6,
bt(2,
None,
bt(4)),
bt(8))))
print(t)
3
├10
│├1
│└7
│ ├5
│ └
└9
├6
│├2
││├
││└4
│└8
└
[16]:
t.sum_rec()
[16]:
55
2.2 height_rec
Let’s say we want to know the height a tree, which is defined as ‘the maximum depth of all the leaves’. We can think recursively as:
the height of a node without children is 0
the height of a node with only a left child is the height of the left node plus one
the height of a node with only a right child is the height of the right node plus one
the height of a node with both left and right children is the maximum of the height of the left node and height of the right node, plus one
Look at the example and try to convince yourself this makes sense:
in purple you see nodes corresponding heights
notice how leaves have all height 0
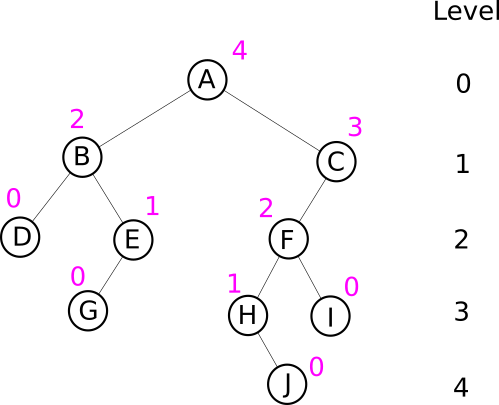
def height_rec(self):
""" RETURN an integer which is the height of the tree
- implement it as recursive call which does NOT modify the tree
NOTE: with big trees a recursive solution would surely exceed
the call stack, but here we don't mind
- A tree with only one node has height zero.
Testing: python3 -m unittest bin_tree_test.HeightRecTest
[ ]:
2.3 depth_rec
def depth_rec(self, level):
"""
- MODIFIES the tree by putting in the data field the provided
value level (which is an integer),
and recursively calls itself on left and right nodes
(if present) passing level + 1
- implement it as a recursive Depth First Search (DFS) traversal
NOTE: with big trees a recursive solution would surely exceed
the call stack, but here we don't mind
- The root of a tree has depth zero.
- does not return anything
Testing: python3 -m unittest bin_tree_test.DepthDfsTest
Example: For example, if we take this tree:
[17]:
t = bt('a', bt('b', bt('c'), None), bt('d', None, bt('e', bt('f'))))
print(t)
a
├b
│├c
│└
└d
├
└e
├f
└
After a call do depth_rec on t passing 0 as starting level, all letters will be substituted by the tree depth at that point:
[18]:
t.depth_rec(0)
[19]:
print(t)
0
├1
│├2
│└
└1
├
└2
├3
└
2.4 contains_rec
def contains_rec(self, item):
""" RETURN True if at least one node in the tree has data equal
to item, otherwise RETURN False.
- implement it as a recursive Depth First Search (DFS) traversal
NOTE: with big trees a recursive solution would surely exceed
the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.ContainsRecTest
Example:
[20]:
t = bt('a',
bt('b',
bt('c'),
bt('d',
None,
bt('e'))),
bt('f',
bt('g',
bt('h')),
bt('i')))
[21]:
print(t)
a
├b
│├c
│└d
│ ├
│ └e
└f
├g
│├h
│└
└i
[22]:
t.contains_rec('g')
[22]:
True
[23]:
t.contains_rec('z')
[23]:
False
2.5 join_rec
def join_rec(self):
""" Supposing the tree nodes hold a character each, RETURN a STRING
holding all characters IN-ORDER
- implement it as a recursive Depth First Search (DFS) traversal
NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.JoinRecTest
[24]:
t = bt('e',
bt('b',
bt('a'),
bt('c',
None,
bt('d'))),
bt('h',
bt('g',
bt('f')),
bt('i')))
[25]:
print(t)
e
├b
│├a
│└c
│ ├
│ └d
└h
├g
│├f
│└
└i
[26]:
t.join_rec()
[26]:
'abcdefghi'
2.6 fun_rec
def fun_rec(self):
""" Supposing the tree nodes hold expressions which can either be
functions or single variables, RETURN a string holding
the complete formula with needed parenthesis.
- implement it as a recursive Depth First Search (DFS)
PRE-ORDER visit
- NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.FunRecTest
Example:
[27]:
t = bt('f',
bt('g',
bt('x'),
bt('y')),
bt('f',
bt('h',
bt('z')),
bt('w')))
[28]:
print(t)
f
├g
│├x
│└y
└f
├h
│├z
│└
└w
[29]:
t.fun_rec()
[29]:
'f(g(x,y),f(h(z),w))'
2.7 bin_search_rec
You are given a so-called binary search tree, which holds numbers as data, and all nodes respect this constraint:
if a node A holds a number strictly less than the number held by its parent node B, then node A must be a left child of B
if a node C holds a number greater or equal than its parent node B, then node C must be a right child of B

[30]:
t = bt(7,
bt(3,
bt(2),
bt(6)),
bt(12,
bt(8,
None,
bt(11,
bt(9))),
bt(14,
bt(13))))
print(t)
7
├3
│├2
│└6
└12
├8
│├
│└11
│ ├9
│ └
└14
├13
└
Implement following method:
def bin_search_rec(self, m):
""" Assuming the tree is a binary search tree of integer numbers,
RETURN True if m is present in the tree, False otherwise
- MUST EXECUTE IN O(height(t))
- NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
QUESTION: what is the complexity in worst case scenario?
QUESTION: what is the complexity when tree is balanced?
Testing: python3 -m unittest bin_tree_test.BinSearchRecTest
2.8 univalued_rec
def univalued_rec(self):
""" RETURN True if the tree is univalued, otherwise RETURN False.
- a tree is univalued when all nodes have the same value as data
- MUST execute in O(n) where n is the number of nodes of the tree
- NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.UnivaluedRecTest
Example:
[31]:
t = bt(3, bt(3), bt(3, bt(3, bt(3, None, bt(3)))))
print(t)
3
├3
└3
├3
│├3
││├
││└3
│└
└
[32]:
t.univalued_rec()
[32]:
True
[33]:
t = bt(2, bt(3), bt(6, bt(3, bt(3, None, bt(3)))))
print(t)
2
├3
└6
├3
│├3
││├
││└3
│└
└
[34]:
t.univalued_rec()
[34]:
False
2.9 same_rec
def same_rec(self, other):
""" RETURN True if this binary tree is equal to other binary tree,
otherwise return False.
- MUST execute in O(n) where n is the number of nodes of the tree
- NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
- HINT: defining a helper function
def helper(t1, t2):
which recursively calls itself and assumes both of the
inputs can be None may lead to cleaner code.
"""
Testing: python3 -m unittest bin_tree_test.SameRecTest
2.10 sum_leaves_rec
We will now go looking for leaves, that is, nodes with no children:
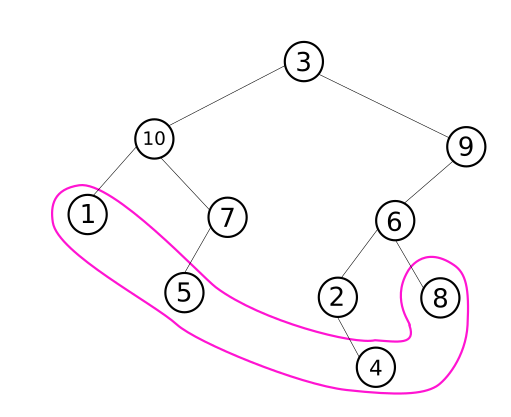
✪✪ Implement this method:
def sum_leaves_rec(self):
""" Supposing the tree holds integer numbers in all nodes,
RETURN the sum of ONLY the numbers in the leaves.
- a root with no children is considered a leaf
- implement it as a recursive Depth First Search (DFS) traversal
NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.SumLeavesRecTest
Example:
[36]:
t = bt(3,
bt(10,
bt(1),
bt(7,
bt(5))),
bt(9,
bt(6,
bt(2,
None,
bt(4)),
bt(8))))
t.sum_leaves_rec() # 1 + 5 + 4 + 8
[36]:
18
2.11 schedule_rec
Suppose the nodes of a binary tree represent tasks (nodes data is the task label). Each task may have up to two subtasks, represented by its children. To be declared as completed, each task requires first the completion of all of its subtasks.
We want to create a schedule of tasks, so that to declare completed the task at the root of the tree, before all tasks below it must be completed, specifically first the tasks on the left side, and then the tasks on the right side. If you apply this reasoning recursively, you can obtain a schedule of tasks to be executed.
def schedule_rec(self):
""" RETURN a list of task labels in the order they will be completed.
- Implement it with recursive calls.
- MUST run in O(n) where n is the size of the tree
NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.ScheduleRecTest
Example:
For this tree, it should return the schedule ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i']
[37]:
from bin_tree_sol import *
from bin_tree_test import bt
[38]:
tasks = bt('i',
bt('d',
bt('b',
bt('a')),
bt('c')),
bt('h',
bt('f',
None,
bt('e')),
bt('g')))
[39]:
print(tasks)
i
├d
│├b
││├a
││└
│└c
└h
├f
│├
│└e
└g
[40]:
tasks.schedule_rec()
[40]:
['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i']
2.12 paths
We define a data path from a node \(v\) to a node \(w\) as the sequence of all nodes data we can collect going from node \(v\) included to node \(w\) included.
Let’s take an example tree:
[41]:
from bin_tree_sol import *
from bin_tree_test import bt
t = bt('a',
bt('b',
bt('d',
bt('h')),
bt('e')),
bt('c',
bt('f',
None,
bt('i',
bt('l'),
bt('m'))),
bt('g')))
from sciprog import draw_bt
draw_bt(t)
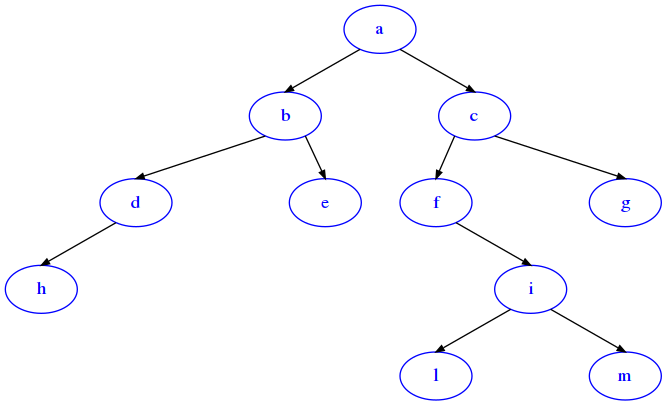
Suppose we want to write a method to RETURN a list of all possible data paths from the root to each leaf. In this case, the paths would be:
[42]:
t.paths_slow_rec()
[42]:
[['a', 'b', 'd', 'h'],
['a', 'b', 'e'],
['a', 'c', 'f', 'i', 'l'],
['a', 'c', 'f', 'i', 'm'],
['a', 'c', 'g']]
To solve the problem we can reason recursively:
if a node \(p\) has no children, then there is only one path from it to itself, so we return
[ [p._data] ](a list of one path)if a node \(p\) has a left child \(l\), a recursive call to
p._left.paths_slow_rec()would produce all paths starting fromp._leftand going to leaves: to obtain all paths starting frompand passing through the left node, we would simply need to prependp._datato all lists obtained from the recursive callfor the right node, the reasoning would be similar
at the end of the algorithm, you would need to collect all processed lists obtained before in a single big list to return
In worst case scenario, what would the complexity be? Let’s see a degenerate tree which is all on a single right branch except interleved small left branches like this:
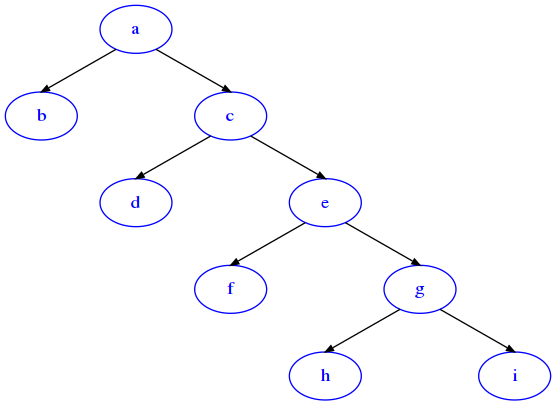
Odd nodes will have to be present in these number of paths:
Even nodes \(b\), \(d\), … would be leaves thus present only in one path each.
So in this worst case we would need at least \(O(n^2)\) to produce the required number of cells with any algorithm.
2.12.1 paths_slow_rec
If we apply the afore mentioned reasoning directly, thus prepending stuff to the obtained results from recursive calls with + operator or .extend(), we would keep rewriting results obtained from recurrent calls into new lists, ending up with an \(O(n^3)\) algorithm.
To get an idea of the problem, for a first version this can be fine as long as we are aware of the hidden costs, so:
USE
+operator or.extendmethod to augment listsDO NOT use
.append(we will reserve it for the fast implementation)
def paths_slow_rec(self):
""" RETURN a list of all paths from this node to the each leaf.
A path is a list which holds the nodes data found while
traversing the tree.
- for this slow version, you can only use + operator or .extend()
method which will bring an O(n^3) complexity
- implement it as recursive call
NOTE: with big trees a recursive solution would surely exceed
the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.PathsSlowRecTest
Example:
[44]:
t = bt('a',
bt('b',
bt('d',
bt('h')),
bt('e')),
bt('c',
bt('f',
None,
bt('i',
bt('l'),
bt('m'))),
bt('g')))
t.paths_slow_rec()
[44]:
[['a', 'b', 'd', 'h'],
['a', 'b', 'e'],
['a', 'c', 'f', 'i', 'l'],
['a', 'c', 'f', 'i', 'm'],
['a', 'c', 'g']]
2.12.2 paths_fast_rec
The previous version is expensive, so let’s try to implement a faster one by only using append() on results produced by recursive calls.
you will also need to implement a helper method.
notice lists this way will come up reversed, you will need to fix them before final return
def _paths_fast_helper(self):
""" DO NOT use + operator nor .extend() method
"""
def paths_fast_rec(self):
""" RETURN a list of all paths from this node to the each leaf.
A path is a list which holds the nodes data found while traversing
the tree.
- DO NOT use + operator nor .extend() method
- MUST work in O(n^2) where n is the number of nodes in the tree
- implement it as recursive call
NOTE: with big trees a recursive solution would surely exceed
the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.PathsFastRecTest
Example:
[45]:
t = bt('a',
bt('b',
bt('d',
bt('h')),
bt('e')),
bt('c',
bt('f',
None,
bt('i',
bt('l'),
bt('m'))),
bt('g')))
t.paths_fast_rec()
[45]:
[['a', 'b', 'd', 'h'],
['a', 'b', 'e'],
['a', 'c', 'f', 'i', 'l'],
['a', 'c', 'f', 'i', 'm'],
['a', 'c', 'g']]
3. Stack visit
To avoid getting ‘Recursion limit exceeded’ errors which can happen with Python, instead of using recursion we can implement tree operations with a while cycle and a stack (or a queue, depending on the case).
Typically, in these algorithms you follow this recipe:
at the beginning you put inside the stack the current node on which the method is called
you keep executing the while until the stack is empty
inside the while, you pop the stack and do some processing on the popped node data
if the node has children, you put them on the stack
We will try to reimplement this way methods we’ve already seen.
3.1 sum_stack
Implement sum_stack
def sum_stack(self):
""" Supposing the tree holds integer numbers in all nodes,
RETURN the sum of the numbers.
- DO *NOT* use recursion
- implement it with a while and a stack (as a python list)
- In the stack place nodes to process
"""
Testing: python3 -m unittest bin_tree_test.SumStackTest

3.2 height_stack
The idea of this function is not that different from the Tasks do_level exercise we’ve seen in the lab about stacks
def height_stack(self):
""" RETURN an integer which is the height of the tree
- A tree with only one node has height zero.
- DO *NOT* use recursion
- implement it with a while and a stack (as a python list).
- In the stack place *tuples* holding a node *and* its level
"""
Testing: python3 -m unittest bin_tree_test.HeightStackTest

3.3 leaves_stack
✪✪✪ Implement this method:
def leaves_stack(self):
""" RETURN a list holding the *data* of all the leaves of the tree,
in left to right order.
- a root with no children is considered a leaf
- DO *NOT* use recursion
- implement it with a while and a stack (as a Python list)
"""
Testing: python3 -m unittest bin_tree_test.LeavesStackTest
Example:
[46]:
t = bt('a',
bt('b',
bt('c'),
bt('d',
None,
bt('e'))),
bt('f',
bt('g',
bt('h')),
bt('i')))
t.leaves_stack()
[46]:
['c', 'e', 'h', 'i']
3.4 swap_stack
Implement this method:
def swap_stack(self, a, b):
""" Given two elements a and b, locates the two nodes where they are contained
and swaps *only the data* in the found nodes.
- if a or b are not found, raise LookupError
- IMPORTANT 1: assume tree is NOT ordered
- IMPORTANT 2: assume all nodes have different data
- Implement it with a while and a stack
- MUST execute in O(n) where n is the size of the tree
"""
Testing: python3 -m unittest bin_tree_test.SwapStackTest
Example:
[48]:
from bin_tree_test import bt
t = bt('a',
bt('b',
bt('c'),
bt('d')),
bt('e',
None,
bt('f',
bt('g'))))
[49]:
draw_bt(t)

[50]:
t.swap_stack('f', 'b')
[51]:
draw_bt(t)

3.5 is_heap_stack
Implement this method:
def is_heap_stack(self):
""" A tree is a min heap if each node data is less or equal than its children data.
RETURN True if the tree is a min heap, False otherwise
- DO *NOT* use recursion
- implement it with a while and a stack (as a python list)
- MUST run in O(n), where n is the tree size
"""
Testing: python3 -m unittest bin_tree_test
[53]:
from bin_tree_test import bt
from bin_tree_sol import *
t = bt(7,
bt(9,
bt(10,
bt(40)),
bt(14)),
bt(20,
None,
bt(30,
bt(50),
bt(90))))
t.is_heap_stack()
[53]:
True
[54]:
t = bt(7,
bt(9,
bt(10,
bt(40)),
bt(14)),
bt(20,
None,
bt(30,
bt(11),
bt(90))))
t.is_heap_stack()
[54]:
False
3.6 others
Hopefully you got an idea of how stack recursion works, now you could try to implement by yourself previously defined recursive functions, this time using a while and a stack (or a queue, depending on what you are trying to achieve).
4. Queue visit
Let’s see what happens when we visit a tree using a queue instead of a stack:
[55]:
from bin_tree_test import bt
from sciprog import draw_bt
t = bt('a',
bt('b',
bt('d'),
bt('e',
None,
bt('g'))),
bt('c',
bt('f',
bt('h'),
bt('i'))))
draw_bt(t)
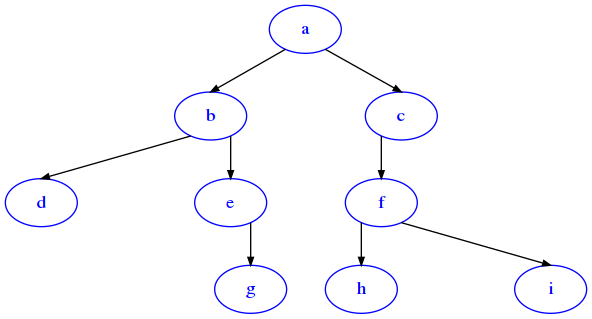
[56]:
from queue import deque
q = deque()
q.append((t, 0)) # we enqueue at the *right*
while len(q) > 0:
node, level = q.popleft() # we dequeue from the *left*
print('level:', level, ' node:', node.data())
if node.left():
q.append((node.left(), level + 1))
if node.right():
q.append((node.right(), level + 1))
level: 0 node: a
level: 1 node: b
level: 1 node: c
level: 2 node: d
level: 2 node: e
level: 2 node: f
level: 3 node: g
level: 3 node: h
level: 3 node: i
We see nodes are traversed level by level, in what can be called a bread-first search (BFS)
Since in this case we enqueued first left and then right child, the traversal in each level will be left-to-right.
Currently we do not provide exercises for levels, but you might need this exploration technique to solve some of the exercises in the references page.
5. Modifying the tree
MODIFY != RETURN
When the text tells you to just MODIFY a tree, you are not supposed to return anything!
Still, you might call return to quit early the method (Python will implicitly return None but that’s fine)
HAVE YOU READ THE POINT ABOVE??
So many students fail their exam because they don’t even properly read the method text.
Again, FIRST look for RETURN / MODIFY keywords, THEN write code accordingly
5.1 mod_sum_rec
Let’s start with a simple method. First just read the text:
def mod_sum_rec(self):
""" Supposing the tree holds integer numbers in all nodes,
MODIFIES each node data becomes the sum of the numbers in all its subtree
- implement it as a recursive Depth First Search (DFS) traversal
NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
QUESTION 1: Should you call something like this inside your method?
return mysum
QUESTION 2: If you just call return like this, is it fine?
return
QUESTION: Given
t = bt(3,
bt(10,
bt(1),
bt(7)))
which of these method calls would make sense?
print(t.mod_sum_rec())
t.mod_sum_rec() print(t.data())

Testing: python3 -m unittest bin_tree_test.ModSumRecTest
Now let’s see some actual call example.
[58]:
t = bt(3,
bt(10,
bt(1),
bt(7,
bt(5))),
bt(9,
bt(6,
bt(2,
None,
bt(4)),
bt(8))))
print(t)
3
├10
│├1
│└7
│ ├5
│ └
└9
├6
│├2
││├
││└4
│└8
└
[59]:
t.mod_sum_rec() # NOTE: returns *nothing* (None is not even displayed in jupyter)
[60]:
print(t) # the actual orginal tree was MODIFIED
55
├23
│├1
│└12
│ ├5
│ └
└29
├20
│├6
││├
││└4
│└8
└
5.2 bin_insert_rec
def bin_insert_rec(self, m):
""" Assuming the tree is a binary search tree of integer numbers,
MODIFIES the tree by inserting a new node with the value m
in the appropriate position. Node is always added as a leaf.
- MUST EXECUTE IN O(height(t))
- NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.BinInsertRecTest
Example:
[61]:
t = bt(7)
print(t)
7
[62]:
t.bin_insert_rec(3)
print(t)
7
├3
└
[63]:
t.bin_insert_rec(6)
print(t)
7
├3
│├
│└6
└
[64]:
t.bin_insert_rec(2)
print(t)
7
├3
│├2
│└6
└
[65]:
t.bin_insert_rec(12)
print(t)
7
├3
│├2
│└6
└12
[66]:
t.bin_insert_rec(14)
print(t)
7
├3
│├2
│└6
└12
├
└14
[67]:
t.bin_insert_rec(13)
print(t)
7
├3
│├2
│└6
└12
├
└14
├13
└
[68]:
t.bin_insert_rec(8)
print(t)
7
├3
│├2
│└6
└12
├8
└14
├13
└
[69]:
t.bin_insert_rec(11)
print(t)
7
├3
│├2
│└6
└12
├8
│├
│└11
└14
├13
└
[70]:
t.bin_insert_rec(9)
print(t)
7
├3
│├2
│└6
└12
├8
│├
│└11
│ ├9
│ └
└14
├13
└
5.2 add_row
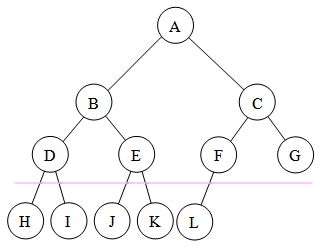
def add_row(self, elems):
""" Takes as input a list of data and MODIFIES the tree by adding
a row of new leaves, each having as data one element of elems,
in order.
- elems size can be less than 2*|leaves|
- if elems size is more than 2*|leaves|, raises ValueError
- for simplicity, you can assume assume self is a perfect
binary tree, that is a binary tree in which all interior nodes
have two children and all leaves have the same depth
- MUST execute in O(n+|elems|) where n is the size of the tree
- DO *NOT* use recursion
- implement it with a while and a stack (as a Python list)
"""
Test: python3 -m unittest bin_tree_test.AddRowTest
Example:
[71]:
from bin_tree_sol import *
from bin_tree_test import bt
t = bt('a',
bt('b',
bt('d'),
bt('e')),
bt('c',
bt('f'),
bt('g')))
print(t)
a
├b
│├d
│└e
└c
├f
└g
[72]:
t.add_row(['h','i','j','k','l'])
[73]:
print(t)
a
├b
│├d
││├h
││└i
│└e
│ ├j
│ └k
└c
├f
│├l
│└
└g
5.3 prune_rec
Implement the method prune_rec:
def prune_rec(self, el):
""" MODIFIES the tree by cutting all the subtrees that have their
root node data equal to el. By 'cutting' we mean they are no longer linked
by the tree on which prune is called.
- if prune is called on a node having data equal to el, raises ValueError
- MUST execute in O(n) where n is the number of nodes of the tree
- NOTE: with big trees a recursive solution would surely
exceed the call stack, but here we don't mind
"""
Testing: python3 -m unittest bin_tree_test.PruneRecTest
Example:
[74]:
from bin_tree_sol import *
from bin_tree_test import bt
[75]:
t = bt('a',
bt('b',
bt('z'),
bt('c',
bt('d'),
bt('z',
None,
bt('e')))),
bt('z',
bt('f'),
bt('z',
None,
bt('g'))))
[76]:
print(t)
a
├b
│├z
│└c
│ ├d
│ └z
│ ├
│ └e
└z
├f
└z
├
└g
[77]:
t.prune_rec('z')
[78]:
print(t)
a
├b
│├
│└c
│ ├d
│ └
└
[79]:
t.prune_rec('c')
[80]:
print(t)
a
├b
└
Trying to prune the root will throw a ValueError:
t.prune_rec('a')
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-27-f8e8fa8a97dd> in <module>()
----> 1 t.prune_rec('a')
ValueError: Tried to prune the tree root !
5.3 family_sum_rec
Implement this method:
def family_sum_rec(self):
""" MODIFIES the tree by adding to each node data its *original* parent and children data
- MUST execute in O(n) where n is the size of the tree
- a recursive implementation is acceptable
- HINT: you will probably want to define a helper function
"""
Testing: python3 -m unittest bin_tree_test.FamilySumRec
Example:
[82]:
from bin_tree_test import bt
t = bt(5,
bt(1,
bt(4,
None,
bt(3)),
bt(2)),
bt(9,
bt(11)))
[83]:
draw_bt(t)

[84]:
t.family_sum_rec()
draw_bt(t)
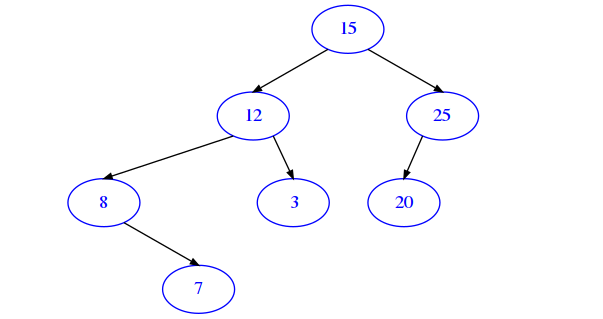
You need to sum to each node data its original parent data + original left child data + original right child data , for example:
Root: 15 = 5 + 0 + 1 + 9
left child of root: 12 = 1 + 5 + 4 + 2
right child of root: 25 = 9 + 5 + 11 + 0
leftmost grandchild of root: 8 = 4 + 1 + 0 + 3
5.4 union_rec
Implement following method:
def union_rec(self, other):
""" Supposing this is a binary tree of integers, takes another binary tree
and MODIFIES self so it becomes the union of the two.
Imagine to overlay the two trees, and:
- whenever two nodes occupy the same position, the self one is updated
by summing the corresponding node data from other
- if other has more nodes than self, create corresponding NEW nodes in self
- a recursive solution is acceptable
- DO *NOT* share nodes between the trees
- DO *NOT* throw away existing nodes in self
- MUST run in O(max(n,m)) where n,m are the number of nodes in self
and other
"""
Testing: python3 -m unittest bin_tree_test.UnionRecTest
Example:
[86]:
from bin_tree_sol import *
from bin_tree_test import bt
[87]:
ta = bt(3,
bt(5,
bt(7,
None,
bt(1,
bt(17)))),
bt(6))
tb = bt(8,
bt(10,
bt(9,
bt(13))),
bt(12,
bt(11,
None,
bt(2)),
bt(4)))
ta.union_rec(tb)
[88]:
print(ta)
11
├15
│├16
││├13
││└1
││ ├17
││ └
│└
└18
├11
│├
│└2
└4
5.5 reconstruct
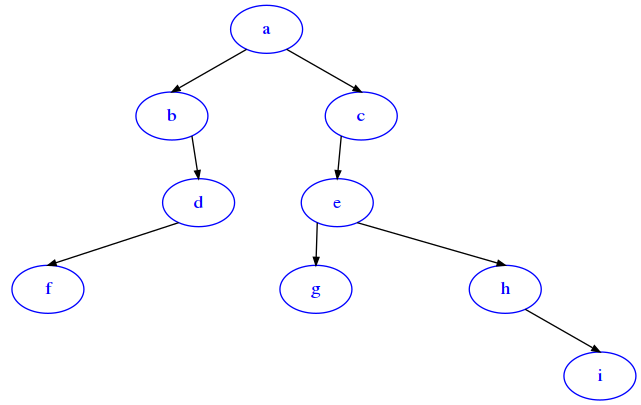
Implement the following function (note it’s external to the class!)
def reconstruct(root, iterator):
""" Takes a root (i.e. 'a') and a sequence of tuples (node, branch, subnode)
*in no particular order*
i.e. ('b','R','c'), ('a','L','b'), ('a','R','b') ...
and RETURN a NEW BinTree reconstructed from such tuples
- node and subnode are represented as node data
- a branch is indicated by either 'L' or 'R'
- MUST perform in O(n) where n is the length of the stream
produced by the iterator
- NOTE: you can read the sequence only once (you are given an iterator)
- in case a branch is repeated (i.e. ('a','L','b') and ('a','L','c'))
the new definition replaces old one
"""
Testing: python3 -m unittest bin_tree_test.ReconstructTest
Example:
[90]:
from bin_tree_sol import *
from bin_tree_test import bt
# note we explicitly pass an iterator just to make sure the implementation reads the sequence only once
t = reconstruct('a', iter([('e','L','g'), ('h','R','i'), ('b','R','d'),
('a','L','b'), ('d','L','f'), ('a','R','c'),
('e','R','h'), ('c', 'L', 'e')]))
[91]:
from sciprog import draw_bt
draw_bt(t)
[ ]: