Exam - Wed 10, Feb 2021

Scientific Programming - Data Science @ University of Trento

Download exercises and solutions

Part A - Wikispeedia

NOTICE: this part of the exam was ported to softpython website

There you can find a more curated version (notice it may be longer than here)

Wikispeedia is a fun game where you are given (or can choose) a source and a target Wikipedia page, and you are asked to reach target page by only clicking links you find along the pages you visit. These click paths provide valuable information regarding human behaviour and the semantic connection between different topics. You will analyze a dataset of such paths.

Data source: https://snap.stanford.edu/data/wikispeedia.html

  • Robert West and Jure Leskovec: Human Wayfinding in Information Networks. 21st International World Wide Web Conference (WWW), 2012.

  • Robert West, Joelle Pineau, and Doina Precup: Wikispeedia: An Online Game for Inferring Semantic Distances between Concepts. 21st International Joint Conference on Artificial Intelligence (IJCAI), 2009.

Open Jupyter and start editing this notebook exam-2021-02-10.ipynb

[2]:

import pandas as pd
import numpy as np
pd.options.display.max_colwidth = None
df = pd.read_csv('paths_finished.tsv', encoding='UTF-8', skiprows=16, header=None, sep='\t')

Each row of the dataset paths_finished.tsv is a user session, where user navigates from start page to end page. Columns are hashedIpAddress, timestamp, durationInSec, path and rating.

We define a session group as all sessions which have same start page and same end page, for example all these paths start with Linguistics and end in Rome:

[3]:

df[5890:5902]

[3]:
0 1 2 3 4
5890 2f8c281d5e0b0e93 1248913182 106 Linguistics;Philosophy;Aristotle;Ancient_Greece;Italy;Rome 3.0
5891 389b67fa365b727a 1249604227 89 Linguistics;Language;English_language;Latin;Rome 2.0
5892 0299542414c3f20a 1257970576 94 Linguistics;Philosophy;Plato;Latin;Rome NaN
5893 2b6e83d366a7514d 1260188882 113 Linguistics;Philosophy;Thomas_Aquinas;Italy;Rome 2.0
5894 0d57c8c57d75e2f5 1282028286 153 Linguistics;Language;Spanish_language;Vulgar_Latin;Roman_Empire;Rome NaN
5895 0d57c8c57d75e2f5 1295244051 62 Linguistics;Philosophy;Socrates;Ancient_Greece;Ancient_Rome;Rome 1.0
5896 772843f73d9cf93d 1307880434 177 Linguistics;Language;German_language;Latin_alphabet;<;Italy;Rome NaN
5897 654430d34a08a0f5 1339755238 81 Linguistics;Philosophy;Augustine_of_Hippo;Italy;Rome 2.0
5898 12470aee3d5ad152 1344167616 40 Linguistics;Philosophy;Plato;Italy;Rome NaN
5899 6365b049395c53ce 1345421532 67 Linguistics;Culture;Ancient_Rome;Rome 1.0
5900 05786cb24102850d 1347671980 65 Linguistics;Language;English_language;Latin;Rome 2.0
5901 369a3f7e77700217 1349302559 56 Linguistics;Language;English_language;Latin;Rome NaN

In this other session group, all sessions start with Pikachu and end with Sun:

[4]:

df[45121:45138]

[4]:
0 1 2 3 4
45121 0d57c8c57d75e2f5 1278403914 17 Pikachu;North_America;Earth;Planet;Sun 1.0
45122 0d57c8c57d75e2f5 1278403938 42 Pikachu;Tree;Sunlight;Sun NaN
45123 0d57c8c57d75e2f5 1278403972 17 Pikachu;Tree;Plant;<;Sunlight;Sun 1.0
45124 0d57c8c57d75e2f5 1278403991 8 Pikachu;Tree;Sunlight;Sun NaN
45125 0d57c8c57d75e2f5 1278404007 9 Pikachu;Tree;Sunlight;Sun 1.0
45126 0d57c8c57d75e2f5 1278404048 8 Pikachu;Tree;Sunlight;Sun NaN
45127 0d57c8c57d75e2f5 1278404061 16 Pikachu;Tree;Sunlight;Sun NaN
45128 0d57c8c57d75e2f5 1278404065 8 Pikachu;Tree;Sunlight;Sun NaN
45129 0d57c8c57d75e2f5 1278404070 8 Pikachu;Tree;Sunlight;Sun NaN
45130 0d57c8c57d75e2f5 1278404089 8 Pikachu;Tree;Sunlight;Sun NaN
45131 0d57c8c57d75e2f5 1278404095 7 Pikachu;Tree;Sunlight;Sun NaN
45132 0d57c8c57d75e2f5 1278404101 9 Pikachu;Tree;Sunlight;Sun NaN
45133 0d57c8c57d75e2f5 1278404117 6 Pikachu;Tree;Sunlight;Sun NaN
45134 0d57c8c57d75e2f5 1278404124 10 Pikachu;Tree;Sunlight;Sun NaN
45135 0d57c8c57d75e2f5 1278404129 9 Pikachu;Tree;Sunlight;Sun NaN
45136 0d57c8c57d75e2f5 1278404142 7 Pikachu;Tree;Sunlight;Sun NaN
45137 0d57c8c57d75e2f5 1278404145 6 Pikachu;Tree;Sunlight;Sun NaN

A1 filter_back

Whenever a user clicks the Back button, she navigates back one page. This fact is tracked in the data by the presence of a '<' symbol. Write a function which RETURN a NEW path without pages which were navigated back.

NOTE: you can have duplicates even without presence of <, because a user might end up to a previous page just by following circular links. Don’t misuse search methods, I’m watching you }:-{

Show solution
[5]:

def filter_back(path):
    raise Exception('TODO IMPLEMENT ME !')

assert filter_back([]) == []
assert filter_back(['alfa']) == ['alfa']
assert filter_back(['beta','alfa','charlie']) == ['beta','alfa','charlie']

assert filter_back(['charlie', 'tango','<']) == ['charlie']
inp = ['charlie', 'tango','<']
assert filter_back(inp) == ['charlie']  # new
assert inp == ['charlie', 'tango','<']
assert filter_back(['alfa', 'beta', 'charlie','<','<','delta']) == ['alfa','delta']
assert filter_back(['alfa', 'beta', 'charlie','delta','eagle','<','<','golf','<','<','hotel']) \
       == ['alfa','beta','hotel']

# circular paths
assert filter_back(['alfa','beta','alfa','alfa','beta']) ==  ['alfa','beta','alfa','alfa','beta']
assert filter_back(['alfa','beta','alfa','<','charlie','charlie','delta','charlie','<','charlie','delta']) \
       == ['alfa','beta','charlie','charlie','delta','charlie','delta']

A2 load_db

Load the tab-separated file paths_finished.tsv with a CSV Reader. The file has some rows to skip and no column names: parse it and RETURN a list of dictionaries, with hashedIpAddress, timestamp, durationInSec, path and rating as fields:

  • path: convert it with filter_back function

  • timestamp and durationInSec: convert to integer

  • rating: convert to integer, if NULL, set it to None

Show solution
[6]:

import csv

def load_db(filename):
    raise Exception('TODO IMPLEMENT ME !')

sessions_db = load_db('paths_finished.tsv')

sessions_db[:2]

Parsed 51318 sessions

[6]:

[{'hashedIpAddress': '6a3701d319fc3754',
  'timestamp': 1297740409,
  'durationInSec': 166,
  'path': ['14th_century',
   '15th_century',
   '16th_century',
   'Pacific_Ocean',
   'Atlantic_Ocean',
   'Accra',
   'Africa',
   'Atlantic_slave_trade',
   'African_slave_trade'],
  'rating': None},
 {'hashedIpAddress': '3824310e536af032',
  'timestamp': 1344753412,
  'durationInSec': 88,
  'path': ['14th_century',
   'Europe',
   'Africa',
   'Atlantic_slave_trade',
   'African_slave_trade'],
  'rating': 3}]

[7]:

# TESTING
from pprint import pprint
from expected_db import expected_db
for i in range(0, len(expected_db)):
    if expected_db[i] != sessions_db[i]:
        print('\nERROR at index', i, ':')
        print('  ACTUAL:')
        pprint(sessions_db[i])
        print('  EXPECTED:')
        pprint(expected_db[i])
        break

A3 calc_stats

Write a function which takes the sessions db and RETURN a NEW dictionary which maps sessions groups expressed as tuples (start, end) to a dictionary of statistics about them

  • dictionary key: tuple with start,end page

  • sessions: the number of sessions in that group

  • avg_len: the average length (as number of edges) of all paths in the group

  • pages: the total number of DISTINCT pages found among all sessions in that group

  • freqs: a dictionary which maps edges found in all sessions of that group to their count

  • max_freq: the highest count among all freqs

Show solution
[8]:

def calc_stats(sessions):
    raise Exception('TODO IMPLEMENT ME !')

stats_db = calc_stats(sessions_db)


[9]:

# TESTING
from pprint import pprint
from expected_stats_db import expected_stats_db
for t in expected_stats_db:
    if not t in stats_db:
        print('\nERROR: missing key for session group', t)
        break
    elif expected_stats_db[t] != stats_db[t]:
        print('\nERROR at key for session group', t, ':')
        print('  ACTUAL:')
        pprint(stats_db[t])
        print('  EXPECTED:')
        pprint(expected_stats_db[t])
        break

Output excerpt:

[10]:

pprint({ k:stats_db[k] for k in [('Linguistics', 'Rome'), ('Pikachu', 'Sun')]})

{('Linguistics', 'Rome'): {'avg_len': 4.166666666666667,
                           'freqs': {('Ancient_Greece', 'Ancient_Rome'): 1,
                                     ('Ancient_Greece', 'Italy'): 1,
                                     ('Ancient_Rome', 'Rome'): 2,
                                     ('Aristotle', 'Ancient_Greece'): 1,
                                     ('Augustine_of_Hippo', 'Italy'): 1,
                                     ('Culture', 'Ancient_Rome'): 1,
                                     ('English_language', 'Latin'): 3,
                                     ('German_language', 'Italy'): 1,
                                     ('Italy', 'Rome'): 5,
                                     ('Language', 'English_language'): 3,
                                     ('Language', 'German_language'): 1,
                                     ('Language', 'Spanish_language'): 1,
                                     ('Latin', 'Rome'): 4,
                                     ('Linguistics', 'Culture'): 1,
                                     ('Linguistics', 'Language'): 5,
                                     ('Linguistics', 'Philosophy'): 6,
                                     ('Philosophy', 'Aristotle'): 1,
                                     ('Philosophy', 'Augustine_of_Hippo'): 1,
                                     ('Philosophy', 'Plato'): 2,
                                     ('Philosophy', 'Socrates'): 1,
                                     ('Philosophy', 'Thomas_Aquinas'): 1,
                                     ('Plato', 'Italy'): 1,
                                     ('Plato', 'Latin'): 1,
                                     ('Roman_Empire', 'Rome'): 1,
                                     ('Socrates', 'Ancient_Greece'): 1,
                                     ('Spanish_language', 'Vulgar_Latin'): 1,
                                     ('Thomas_Aquinas', 'Italy'): 1,
                                     ('Vulgar_Latin', 'Roman_Empire'): 1},
                           'max_freq': 6,
                           'pages': 19,
                           'sessions': 12},
 ('Pikachu', 'Sun'): {'avg_len': 3.0588235294117645,
                      'freqs': {('Earth', 'Planet'): 1,
                                ('North_America', 'Earth'): 1,
                                ('Pikachu', 'North_America'): 1,
                                ('Pikachu', 'Tree'): 16,
                                ('Planet', 'Sun'): 1,
                                ('Sunlight', 'Sun'): 16,
                                ('Tree', 'Sunlight'): 16},
                      'max_freq': 16,
                      'pages': 7,
                      'sessions': 17}}

A4 plot_network

Given a sessions group (start_page, target_page), we want to display the pages clicked by users for all its sessions. Since some sessions share edges, we will show their click frequency.

  • Set edges attributes 'weight', 'label' as \(freq\), 'penwidth' as \(5 \large \frac{freq}{max\_freq}\) and 'color' as '#45daed'

  • Only display edges (and pages connected by such edges) for which the click count is strictly greater than the given threshold

  • NOTE: when applying a threshold, it’s fine if some nodes don’t appear linked to either source or target

Show solution
[11]:

from sciprog import draw_nx
import networkx as nx

def plot_network(stats, source_page, target_page, threshold=0):
    raise Exception('TODO IMPLEMENT ME !')

plot_network(stats_db,'Linguistics', 'Rome')

Image saved to file:  expected-Linguistics-Rome-0.png
../../../_images/exams_2021-02-10_solutions_exam-2021-02-10-sol_31_1.png 
[12]:

plot_network(stats_db, 'Batman', 'Bible', 0)  # default threshold zero, big graph

Image saved to file:  expected-Batman-Bible-0.png
../../../_images/exams_2021-02-10_solutions_exam-2021-02-10-sol_32_1.png 
[13]:

plot_network(stats_db, 'Batman', 'Bible', 1)   # we take only edges > 1

Image saved to file:  expected-Batman-Bible-1.png
../../../_images/exams_2021-02-10_solutions_exam-2021-02-10-sol_33_1.png

Part B

  • Open Visual Studio Code and start editing the folder on your desktop

B1.1 Theory - Complexity

Write the solution in separate ``theory.txt`` file

Given a list \(L\) of \(n\) elements, please compute the asymptotic computational complexity of the following function, explaining your reasoning.

[15]:

def my_fun(L):
    T = []
    N = len(L)
    for i in range(N):
        cnt = 0
        for j in range(N):
            if  L[i] > L[j]:
                cnt += 1
        T.append(cnt)

    return T

B1.2 Theory - BST

Briefly answer the following questions: what is the Tree data structure. What is a Binary Search Tree (BST)? What can we use a BST for?

B2 Reconstruct BinaryTree

Open bin_tree.py and implement the following function (note it’s external to the class!)

def reconstruct(root, iterator):
    """ Takes a root (i.e. 'a') and a sequence of tuples (node, branch, subnode)
        *in no particular order*
        i.e. ('b','R','c'), ('a','L','b'), ('a','R','b') ...

        and RETURN a NEW BinaryTree reconstructed from such tuples

        - node and subnode are represented as node data
        - a branch is indicated by either 'L' or 'R'

        - MUST perform in O(n) where n is the length of the stream
          produced by the iterator
        - NOTE: you can read the sequence only once (you are given an iterator)
        - in case a branch is repeated (i.e. ('a','L','b') and ('a','L','c'))
          the new definition replaces old one
    """

Testing: python3 -m unittest bin_tree_test.ReconstructTest

Example:

[17]:

from bin_tree_sol import *
from bin_tree_test import bt

# note we explicitly pass an iterator just to make sure the implementation reads the sequence only once
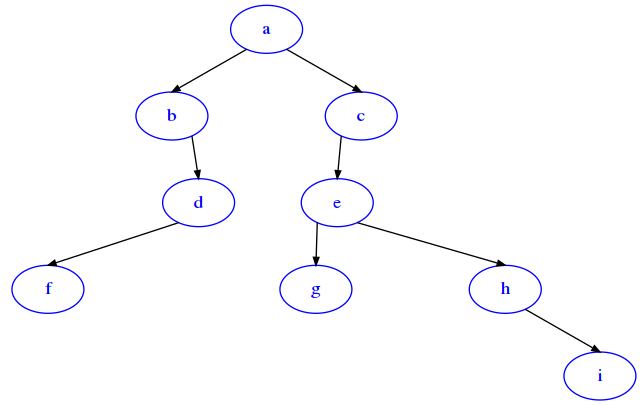
t = reconstruct('a', iter([('e','L','g'), ('h','R','i'), ('b','R','d'),
                           ('a','L','b'), ('d','L','f'), ('a','R','c'),
                           ('e','R','h'), ('c', 'L', 'e')]))

[18]:

from sciprog import draw_bt
draw_bt(t)
../../../_images/exams_2021-02-10_solutions_exam-2021-02-10-sol_43_0.png

B3 Marvelous

Open generic_tree.py and edit this method:

def marvelous(self):
    """ MODIFIES each node data replacing it with the concatenation
        of its leaves data

        - MUST USE a recursive solution
        - assume node data is always a string
    """

Testing: python3 -m unittest generic_tree_test.MarvelousTest

Example: NOTE: leaves may be any character! Here we show them as uppercase but they might also be lowercase.

[20]:

from gen_tree_sol import *
from gen_tree_test import gt

t = gt('a',
          gt('b',
                gt('M'),
                gt('A'),
                gt('R')),
          gt('c',
                gt('e',
                      gt('V'),),
                gt('E')),
          gt('d',
                gt('L'),
                gt('f',
                      gt('O'),
                      gt('U'),),
                gt('S')))

[21]:

print(t)

a
├b
│├M
│├A
│└R
├c
│├e
││└V
│└E
└d
 ├L
 ├f
 │├O
 │└U
 └S

[22]:

t.marvelous()
print(t)

MARVELOUS
├MAR
│├M
│├A
│└R
├VE
│├V
││└V
│└E
└LOUS
 ├L
 ├OU
 │├O
 │└U
 └S

[ ]: