Midterm B - Wed 16, Dec 2020
Scientific Programming - Data Science @ University of Trento
Download exercises and solutions
Introduction
Taking part to this exam erases any vote you had before
What to do
Download
sciprog-ds-2020-12-16-exam.zipand extract it on your desktop.Rename
sciprog-ds-2020-12-16-FIRSTNAME-LASTNAME-IDfolder: put your name, lastname an id number, likesciprog-ds-2020-12-16-john-doe-432432
From now on, you will be editing the files in that folder. At the end of the exam, that is what will be evaluated.
Edit the files following the instructions in this worksheet for each exercise. Each should take max 25 mins, if it takes longer, leave it and try another exercise
When done:
if you have unitn login: zip and send to examina.icts.unitn.it/studente
If you don’t have unitn login: tell instructors and we will download your work manually
Now Open Visual Studio Code and start editing the folder on your desktop
For running tests: open Accessories -> Terminal
B1 Theory
Write the solution in separate ``theory.txt`` file
B1.1. complexity
Given a list L of \(n\geq3\) integer elements, please compute the asymptotic computational complexity of the following function, explaining your reasoning.
def my_fun(L):
for i in range(3, len(L)):
k = 0
R = L[i]
tmp = []
while k < 3:
if k % 2 == 1:
R = R - L[k]
else:
R = R + L[k]
k += 1
tmp.append(R)
return sum(tmp)
B1.2 dag topsort
What is the topological sorting of a directed acyclic graph (DAG)? Briefly describe an algorithm to compute it and provide a possible topological view of the following DAG.

B2 LinkedList pivot
def pivot(self):
"""
Selects first node data as pivot, and then MOVES before the pivot
all the nodes which have data value STRICTLY LESS (<) than the pivot.
Finally, RETURN the number of moved nodes.
IMPORTANT:
- *DO NOT* create new nodes
- nodes < than pivot must be in the reversed order they were found
- nodes >= than pivot will maintain the original order
- MUST EXECUTE in O(n), where n is the list size
"""
Testing: python3 -m unittest linked_list_test.PivotTest
Example:
[2]:
from linked_list_sol import *
from linked_list_test import to_ll
ll = to_ll([7, 12, 1, 3, 8, 9, 6, 4, 7, 2, 10])
[3]:
print(ll)
LinkedList: 7,12,1,3,8,9,6,4,7,2,10
[4]:
res = ll.pivot()
[5]:
res # there were 5 elements strictly less than pivot 7
[5]:
5
Note elements \(< 7\) are in reverse order in which they were found, elements \(\geq7\) are in the original order
[6]:
print(ll)
LinkedList: 2,4,6,3,1,7,12,8,9,7,10
B3 swap_stack
Open bin_tree.py and implement this method:
def swap_stack(self, a, b):
""" Given two elements a and b, locates the two nodes where they are contained
and swaps *only the data* in the found nodes.
- if a or b are not found, raise LookupError
- IMPORTANT 1: assume tree is NOT ordered
- IMPORTANT 2: assume all nodes have different data
- Implement it with a while and a stack
- MUST execute in O(n) where n is the size of the tree
"""
Testing: python3 -m unittest bin_tree_test.SwapStackTest
Example:
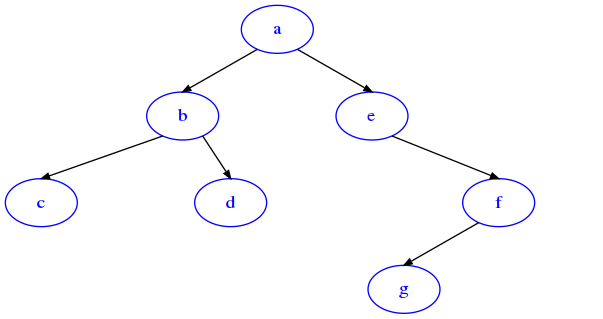
[7]:
from bin_tree_test import bt
t = bt('a',
bt('b',
bt('c'),
bt('d')),
bt('e',
None,
bt('f',
bt('g'))))
[8]:
draw_bt(t)
[9]:
t.swap_stack('f', 'b')
[10]:
draw_bt(t)

B4 family_sum_rec
Open bin_tree.py and implement this method:
def family_sum_rec(self):
""" MODIFIES the tree by adding to each node data its *original* parent and children data
- MUST execute in O(n) where n is the size of the tree
- A recursive implementation is acceptable
- HINT: you will probably want to define a helper function
"""
Testing: python3 -m unittest bin_tree_test.FamilySumRec
Example:
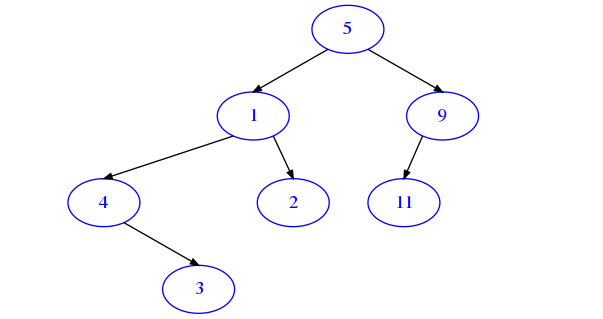
[11]:
from bin_tree_test import bt
t = bt(5,
bt(1,
bt(4,
None,
bt(3)),
bt(2)),
bt(9,
bt(11)))
[12]:
draw_bt(t)
[13]:
t.family_sum_rec()
draw_bt(t)

You need to sum to each node data its original parent data + original left child data + original right child data , for example:
Root: 15 = 5 + 0 + 1 + 9
left child of root: 12 = 1 + 5 + 4 + 2
right child of root: 25 = 9 + 5 + 11 + 0
leftmost grandchild of root: 8 = 4 + 1 + 0 + 3
[ ]: