Midterm - Fri 16 Nov 2018
Scientific Programming - Data Science Master @ University of Trento
Download exercises and solution
Introduction
What to do
Download
sciprog-ds-2018-11-16-exam.zipand extract it on your desktop. Folder content should be like this:
sciprog-ds-2018-11-16-FIRSTNAME-LASTNAME-ID
exam-2018-11-16.ipynb
jupman.py
sciprog.py
Rename
sciprog-ds-2018-11-16-FIRSTNAME-LASTNAME-IDfolder: put your name, lastname an id number, likesciprog-ds-2018-11-16-john-doe-432432
From now on, you will be editing the files in that folder. At the end of the exam, that is what will be evaluated.
Edit the files following the instructions in this worksheet for each exercise.
When done:
if you have unitn login: zip and send to examina.icts.unitn.it
If you don’t have unitn login: tell instructors and we will download your work manually
A1 union
✪✪ When we talk about the union of two graphs, we intend the graph having union of verteces of both graphs and having as edges the union of edges of both graphs. In this exercise, we have two graphs as list of lists with boolean edges. To simplify we suppose they have the same vertices but possibly different edges, and we want to calculate the union as a new graph.
For example, if we have a graph ma like this:
[2]:
ma = [
[True, False, False],
[False, True, False],
[True, False, False]
]
[3]:
draw_mat(ma)

And another mb like this:
[4]:
mb = [
[True, True, False],
[False, False, True],
[False, True, False]
]
[5]:
draw_mat(mb)
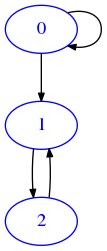
The result of calling union(ma, mb) will be the following:
[19]:
res = [[True, True, False], [False, True, True], [True, True, False]]
which will be displayed as
[20]:
draw_mat(res)
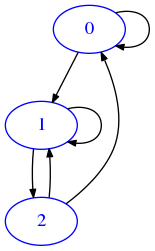
So we get same verteces and edges from both ma and mb
[6]:
def union(mata, matb):
""" Takes two graphs represented as nxn matrices of lists of lists with boolean edges,
and RETURN a NEW matrix which is the union of both graphs
if mata row number is different from matb, raises ValueError
"""
raise Exception('TODO IMPLEMENT ME !')
try:
union([[False],[False]], [[False]])
raise Exception("Shouldn't arrive here !")
except ValueError:
"test passed"
try:
union([[False]], [[False],[False]])
raise Exception("Shouldn't arrive here !")
except ValueError:
"test passed"
ma1 = [
[False]
]
mb1 = [
[False]
]
assert union(ma1, mb1) == [
[False]
]
ma2 = [
[False]
]
mb2 = [
[True]
]
assert union(ma2, mb2) == [
[True]
]
ma3 = [
[True]
]
mb3 = [
[False]
]
assert union(ma3, mb3) == [
[True]
]
ma4 = [
[True]
]
mb4 = [
[True]
]
assert union(ma4, mb4) == [
[True]
]
ma5 = [
[False, False, False],
[False, False, False],
[False, False, False]
]
mb5 = [
[True, False, True],
[False, True, True],
[False, False, False]
]
assert union(ma5, mb5) == [
[True, False, True],
[False, True, True],
[False, False, False]
]
ma6 = [
[True, False, True],
[False, True, True],
[False, False, False]
]
mb6 = [
[False, False, False],
[False, False, False],
[False, False, False]
]
assert union(ma6, mb6) == [
[True, False, True],
[False, True, True],
[False, False, False]
]
ma7 = [
[True, False, False],
[False, True, False],
[True, False, False]
]
mb7 = [
[True, True, False],
[False, False, True],
[False, True, False]
]
assert union(ma7, mb7) == [
[True, True, False],
[False, True, True],
[True, True, False]
]
A2 surjective
✪✪ If we consider a graph as a nxn binary relation where the domain is the same as the codomain, such relation is called surjective if every node is reached by at least one edge.
For example, G1 here is surjective, because there is at least one edge reaching into each node (self-loops as in 0 node also count as incoming edges)
[7]:
G1 = [
[True, True, False, False],
[False, False, False, True],
[False, True, True, False],
[False, True, True, True],
]
[8]:
draw_mat(G1)

G2 down here instead does not represent a surjective relation, as there is at least one node ( 2 in our case) which does not have any incoming edge:
[9]:
G2 = [
[True, True, False, False],
[False, False, False, True],
[False, True, False, False],
[False, True, False, False],
]
[10]:
draw_mat(G2)

[11]:
def surjective(mat):
""" RETURN True if provided graph mat as list of boolean lists is an
nxn surjective binary relation, otherwise return False
"""
raise Exception('TODO IMPLEMENT ME !')
m1 = [
[False]
]
assert surjective(m1) == False
m2 = [
[True]
]
assert surjective(m2) == True
m3 = [
[True, False],
[False, False],
]
assert surjective(m3) == False
m4 = [
[False, True],
[False, False],
]
assert surjective(m4) == False
m5 = [
[False, False],
[True, False],
]
assert surjective(m5) == False
m6 = [
[False, False],
[False, True],
]
assert surjective(m6) == False
m7 = [
[True, False],
[True, False],
]
assert surjective(m7) == False
m8 = [
[True, False],
[False, True],
]
assert surjective(m8) == True
m9 = [
[True, True],
[False, True],
]
assert surjective(m9) == True
m10 = [
[True, True, False, False],
[False, False, False, True],
[False, True, False, False],
[False, True, False, False],
]
assert surjective(m10) == False
m11 = [
[True, True, False, False],
[False, False, False, True],
[False, True, True, False],
[False, True, True, True],
]
assert surjective(m11) == True
A3 ediff
✪✪✪ The edge difference of two graphs ediff(da,db) is a graph with the edges of the first except the edges of the second. For simplicity, here we consider only graphs having the same verteces but possibly different edges. This time we will try operate on graphs represented as dictionaries of adjacency lists.
For example, if we have
[12]:
da = {
'a':['a','c'],
'b':['b', 'c'],
'c':['b','c']
}
[13]:
draw_adj(da)

and
[14]:
db = {
'a':['c'],
'b':['a','b', 'c'],
'c':['a']
}
[15]:
draw_adj(db)

The result of calling ediff(da,db) will be:
[16]:
res = {
'a':['a'],
'b':[],
'c':['b','c']
}
Which can be shown as
[17]:
draw_adj(res)

[18]:
def ediff(da,db):
""" Takes two graphs as dictionaries of adjacency lists da and db, and
RETURN a NEW graph as dictionary of adjacency lists, containing the same vertices of da,
and the edges of da except the edges of db.
- As order of elements within the adjacency lists, use the same order as found in da.
- We assume all verteces in da and db are represented in the keys (even if they have
no outgoing edge), and that da and db have the same keys
EXAMPLE:
da = {
'a':['a','c'],
'b':['b', 'c'],
'c':['b','c']
}
db = {
'a':['c'],
'b':['a','b', 'c'],
'c':['a']
}
assert ediff(da, db) == {
'a':['a'],
'b':[],
'c':['b','c']
}
"""
raise Exception('TODO IMPLEMENT ME !')
da1 = {
'a': []
}
db1 = {
'a': []
}
assert ediff(da1, db1) == {
'a': []
}
da2 = {
'a': []
}
db2 = {
'a': ['a']
}
assert ediff(da2, db2) == {
'a': []
}
da3 = {
'a': ['a']
}
db3 = {
'a': []
}
assert ediff(da3, db3) == {
'a': ['a']
}
da4 = {
'a': ['a']
}
db4 = {
'a': ['a']
}
assert ediff(da4, db4) == {
'a': []
}
da5 = {
'a':['b'],
'b':[]
}
db5 = {
'a':['b'],
'b':[]
}
assert ediff(da5, db5) == {
'a':[],
'b':[]
}
da6 = {
'a':['b'],
'b':[]
}
db6 = {
'a':[],
'b':[]
}
assert ediff(da6, db6) == {
'a':['b'],
'b':[]
}
da7 = {
'a':['a','b'],
'b':[]
}
db7 = {
'a':['a'],
'b':[]
}
assert ediff(da7, db7) == {
'a':['b'],
'b':[]
}
da8 = {
'a':['a','b'],
'b':['a']
}
db8 = {
'a':['a'],
'b':['b']
}
assert ediff(da8, db8) == {
'a':['b'],
'b':['a']
}
da9 = {
'a':['a','c'],
'b':['b', 'c'],
'c':['b','c']
}
db9 = {
'a':['c'],
'b':['a','b', 'c'],
'c':['a']
}
assert ediff(da9, db9) == {
'a':['a'],
'b':[],
'c':['b','c']
}