Exam - Tue 14, Jan 2021
Scientific Programming - Data Science Master @ University of Trento
Download exercises and solutions
Part A - Witchcraft
NOTICE: this part of the exam was ported to softpython website
There you can find a more curated version (notice it may be longer than here)
The early sixteenth century saw a dramatic rise in awareness and terror of witchcraft in the troubled lands of early modern Scotland: thousands of people were executed, imprisoned, tortured, banished, and had lands and possessions confiscated. Persecution took place in courts of law: you shall analyze the evidence gathered during those dark days.
Data source: Julian Goodare, Lauren Martin, Joyce Miller and Louise Yeoman, ‘The Survey of Scottish Witchcraft’ http://www.shca.ed.ac.uk/witches/ (archived January 2003, accessed ’11/1/2016’).
In particular, we took WDB_Case.csv as published on data.world, which contains cases brought against suspected witches, along with annotations by researchers, mostly as boolean fields.
The dataset has lots of columns, we show here only the relevant ones Case_date, CaseCommonName, Suspects_text and an excerpt of the many boolean columns:
[1]:
import pandas as pd
case_df = pd.read_csv('WDB_Case.csv', encoding='UTF-8')
sel_case_df = case_df[['Case_date', 'CaseCommonName', 'Suspects_text', 'Demonic_p', 'Demonic_s', 'Maleficium_p','Maleficium_s', 'WitchesMeeting']]
sel_case_df[1986:1994]
[1]:
| Case_date | CaseCommonName | Suspects_text | Demonic_p | Demonic_s | Maleficium_p | Maleficium_s | WitchesMeeting | |
|---|---|---|---|---|---|---|---|---|
| 1986 | 29/6/1649 | 3 unnamed witches | 3.0 | 0 | 0 | 0 | 0 | 0 |
| 1987 | 19/8/1590 | Leslie,William | NaN | 0 | 0 | 0 | 1 | 0 |
| 1988 | 1679 | McGuffock,Margaret | NaN | 0 | 0 | 0 | 1 | 0 |
| 1989 | 1679 | Rae,Grissell | NaN | 0 | 0 | 0 | 0 | 0 |
| 1990 | 1679 | Howat,Jonet | NaN | 0 | 0 | 0 | 0 | 0 |
| 1991 | 15/10/1673 | McNicol,Janet | NaN | 1 | 1 | 0 | 1 | 1 |
| 1992 | 4/6/1674 | Clerk,Margaret | NaN | 0 | 0 | 0 | 0 | 0 |
| 1993 | 29/7/1675 | Hendrie,Agnes | NaN | 0 | 1 | 0 | 0 | 1 |
A1 parse_bool_cols
Open Jupyter and start editing this notebook exam-2021-01-14.ipynb
Since boolean columns are so many, as a first step you will build a recognizer for them.
Consider a column as boolean if ALL of its values are either
0or1Parse with CSV DictReader
WARNING: Have you carefully read the text above?
Most students during the exam didn’t, and wrote algorithms which declare a column as boolean as soon as a 0 or a 1 are found and manually discarded columns which didn’t fit their flawed logic (like NamedIndividual).
To avoid getting bad grades for simple exercises, always ask yourself:
Am I sure about the results of my algorithm without looking at the expected solution ? In this case, it should be obvious that if you don’t scan all cells in a column and you still declare it’s boolean you are basically resorting to being lucky.
Am I putting constants in the code (like
'NamedIndividual')? Whenever you have such urge, please ask first for permissionIs the exercise open to interpretation, maybe because it has so many possible weird cases and relative assertions, or is the text pretty clear? In this case the scope was quite definite, so you are expected to find a generic solution which could work with any dataset.
Example (for full output see expected_bool_cols.py):
>>> bool_cols = get_bool_cols('WDB_Case.csv')
>>> print('Found', len(bool_cols), 'cols. EXCERPT:', ' '.join(bool_cols[:17]), '...')
Found 77 cols. EXCERPT:
AdmitLesserCharge AggravatingDisease AnimalDeath AnimalIllness ClaimedBewitched ClaimedNaturalCauses ClaimedPossessed CommunalSex Consulting_p Consulting_s Cursing Dancing DemonicPact Demonic_p Demonic_possess_p Demonic_possess_s Demonic_s ...
[2]:
def get_bool_cols(filename):
"""RETURN a sorted list of all the names of boolean columns"""
raise Exception('TODO IMPLEMENT ME !')
bool_cols = get_bool_cols('WDB_Case.csv')
print('Found', len(bool_cols), 'cols.', 'EXCERPT: ',)
print( ' '.join(bool_cols[:17]), '...')
from expected_bool_cols import expected_bool_cols
if len(bool_cols) != len(expected_bool_cols):
print('ERROR! different lengths: bools_cols: %s expected_bools_cols: %s' % (len(bool_cols), len(expected_bool_cols)))
else:
for i in range(len(expected_bool_cols)):
if bool_cols[i] != expected_bool_cols[i]:
print('ERROR at index', i, ':')
print(' ACTUAL:', repr(bool_cols[i]))
print(' EXPECTED:', repr(expected_bool_cols[i]))
A2 fix_date
Implement fix_date, which takes a possibly partial date as a string d/m/yyyy and RETURN a string formatted as mm/dd/yyyy. If data is missing, omits it in the output as well, see examples.
[3]:
def fix_date(d):
raise Exception('TODO IMPLEMENT ME !')
assert fix_date('2/8/1649') == '08/02/1649'
assert fix_date('25/4/1627') == '04/25/1627'
assert fix_date('6/11/1629') == '11/06/1629'
assert fix_date('12/1649') == '12/1649'
assert fix_date('7/1652') == '07/1652'
assert fix_date('1560') == '1560'
assert fix_date('') == ''
# Note there is a damned extra space in the dataset (Oswald,Katharine)
assert fix_date('13/11/ 1629') == '11/13/1629'
A3 parse_db
Given a CSV of cases, outputs a list of dictionaries (parse with CSV DictReader), each representing a case with these fields:
name: the isolated name of the witch taken fromCaseCommonNamecolumn if parseable, otherwise the full cell contentsurname: the isolated surname of the witch taken fromCaseCommonNamecolumn if parseable, otherwise empty stringcase_date:Case_datecolumn corrected withfix_datesuspects: number of suspects as integer, to be taken from the columnSuspects_text. If column is empty, use1
primary, secondary and tags fields are to be filled with names of boolean columns for which the corresponding cell is marked with '1' according to these criteria:
primary: a single string as follows: if a column ending with_pis marked'1', this field contains that column name without the'_p'. If column name is'NotEnoughInfo_p'or in other cases, useNone.secondary: sorted column names ending with_s. If col name is'NotEnoughInfo_s'or it’s already present asprimary, it’s discarded. Remove trailing_sfrom values in the list.tags: sorted column names which are not primary nor secondary
Example (full output is in expected_cases_db.py):
>>> cases_db = parse_db('WDB_Case.csv')
>>> cases_db[1991:1994]
[{'primary': 'Demonic',
'secondary': ['ImplicatedByAnother', 'Maleficium', 'UNorthodoxRelPract'],
'tags': ['DevilPresent', 'UnorthodoxReligiousPractice', 'WitchesMeeting'],
'name': 'Janet',
'surname': 'McNicol',
'suspects': 1,
'case_date': '10/15/1673'},
{'primary': None,
'secondary': [],
'tags': [],
'name': 'Margaret',
'surname': 'Clerk',
'suspects': 1,
'case_date': '06/04/1674'},
{'primary': None,
'secondary': ['Demonic'],
'tags': ['Dancing', 'DevilPresent', 'Singing', 'WitchesMeeting'],
'name': 'Agnes',
'surname': 'Hendrie',
'suspects': 1,
'case_date': '07/29/1675'}]
[4]:
import csv
def parse_db(filename):
raise Exception('TODO IMPLEMENT ME !')
cases_db = parse_db('WDB_Case.csv')
cases_db[1991:1994]
[5]:
# TESTS
assert cases_db[0]['primary'] == None
assert cases_db[0]['secondary'] == []
assert cases_db[0]['name'] == '3 unnamed witches'
assert cases_db[0]['surname'] == ''
assert cases_db[0]['suspects'] == 3 # int !
assert cases_db[0]['case_date'] == '08/02/1649'
assert cases_db[1]['primary'] == None
assert cases_db[1]['secondary'] == ['ImplicatedByAnother']
assert cases_db[1]['tags'] == []
assert cases_db[1]['name'] == 'Cristine'
assert cases_db[1]['surname'] == 'Kerington'
assert cases_db[1]['suspects'] == 1 # Suspects_text is '', we put 1
assert cases_db[1]['case_date'] == '05/08/1591'
assert cases_db[1991]['primary'] == 'Demonic'
#NOTE: since 'Demonic' is already 'primary', we removed it from 'secondary'
assert cases_db[1991]['secondary'] == ['ImplicatedByAnother', 'Maleficium', 'UNorthodoxRelPract']
assert cases_db[1991]['tags'] == ['DevilPresent', 'UnorthodoxReligiousPractice', 'WitchesMeeting']
assert cases_db[1991]['name'] == 'Janet'
assert cases_db[1991]['surname'] == 'McNicol'
assert cases_db[1991]['suspects'] == 1 # Suspects_text is '', we put 1
assert cases_db[1991]['case_date'] == '10/15/1673'
assert cases_db[0]['case_date'] == '08/02/1649' # 2/8/1649
assert cases_db[1143]['case_date'] == '1560' # 1560
assert cases_db[924]['case_date'] == '07/1652' # 7/1652
assert cases_db[491]['suspects'] == 15 # 15
#composite name
assert cases_db[249]['name'] == 'Francis' # "Stewart, Earl of Bothwell,Francis"
assert cases_db[249]['surname'] == 'Stewart, Earl of Bothwell'
from expected_cases_db import expected_cases_db
from pprint import pprint
for i in range(len(expected_cases_db)):
if cases_db[i] != expected_cases_db[i]:
print('ERROR at index %s!' % i)
print('ACTUAL:')
pprint(cases_db[i])
print('EXPECTED:', )
pprint(expected_cases_db[i])
if len(cases_db) != len(expected_cases_db):
print('ERROR! different lengths: cases_db: %s expected_cases_db: %s' % (len(cases_db), len(expected_cases_db)))
assert cases_db == expected_cases_db
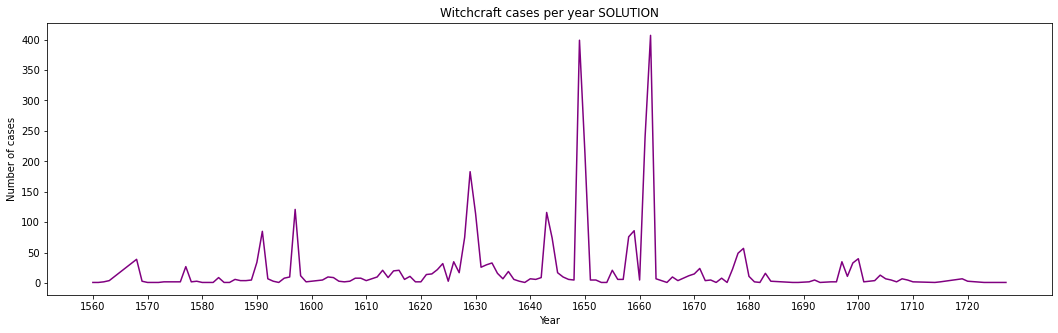
A4 plot_cases
Given the previously computed db, plot the number of cases per year.
plot the ticks with 10 years intervals, according to the actual data (DO NOT use constants like
1560!!)careful some cases have no year

[6]:
def plot_cases(db):
raise Exception('TODO IMPLEMENT ME !')
plot_cases(cases_db)
Part B
B1.1 Theory - Complexity
Write the solution in separate ``theory.txt`` file
Given a list \(L\) of \(n\) elements, please compute the asymptotic computational complexity of the following function, explaining your reasoning.
def my_fun(L):
n = len(L)
if n <= 1:
return 1
else:
L1 = L[0:n//2]
L2 = L[n//2:]
a = my_fun(L1) + min(L1)
b = my_fun(L2) + min(L2)
return max(a, b)
B1.2 Theory - Graph
Briefly describe what a BFS visit of a graph is. Please provide the order of visited nodes of a possible BFS visit on the following graph (starting from node ‘a’):

B2 Bank
WARNING: AN UPDATED VERSION OF THIS EXERCISE CAN BE FOUND HERE
A bank stores all its transactions in a log: possible types of transactions are opening an account, transfering some amount of money, withdrawal, etc. For simplicity, we represent each transaction type with a character, and in the log which is a Python list we put only such characters (we don’t care about their meaning).
The bank knows some sequences of events are extremely rare, and probably denote suspicious activity. For simplicitly, we assume such sequences only contain two transactions and represent them in tuples called biseqs.
NOTE: a biseq can occur multiple times, but you can consider the number of repetitions negligible with respect to log size.
THESE EXERCISES ARE ABOUT CUSTOM INDEXING, NOT STRINGS: DO NOT convert everything to a string, use regexes, nor use string methods like .index(), .replace(), etc
B2.1 constructor, log and pos
Implement following methods, adding some appropriate indexing data structure.
BEFORE IMPLEMENTING, DOUBLE CHECK COMPLEXITY REQUIREMENTS!
The idea is that given an entire biseq (not just the first character !), we want to find all of its (rare) occurrences very fast in \(O(1)\)
Since performance is important here, passing tests does not imply your work is correct!
class Bank:
def __init__(self):
""" Initializes an empty bank
Add a data structure of your choice for indexing the log
"""
self._trans = []
raise Exception("TODO IMPLEMENT ME!")
def log(self, transaction):
""" Appends transaction to the log
- REMEMBER to also update the index
- MUST EXECUTE IN O(1)
"""
def pos(self, biseq):
""" RETURN a NEW list with all the indeces where the sequence of
two transactions can be found
- MUST execute in O(1)
"""
Testing: python3 -m unittest bank_test.LogTest
Example:
[7]:
from bank_sol import *
bank = Bank()
print(bank)
Bank:
[8]:
bank.log('a')
[9]:
print(bank)
Bank: a
[10]:
print(bank.pos( ('a','b') )) # <-- a biseq is a tuple
[]
[11]:
bank.log('b')
[12]:
print(bank.pos( ('a','b') ))
[0]
[13]:
bank.log('a')
bank.log('a')
bank.log('a')
bank.log('a')
bank.log('b')
print(bank)
Bank: a,b,a,a,a,a,b
[14]:
print(bank.pos(('a','b')))
[0, 5]
[15]:
print(bank.pos(('a','a')))
[2, 3, 4]
B2.2 revert
def revert(self):
""" Completely eliminates last transaction and RETURN it
- if bank is empty, raises IndexError
- REMEMBER to update any index referring to it
- *MUST* EXECUTE IN O(1)
"""
Testing: python3 -m unittest RevertTest
Example:
[16]:
bank = Bank()
bank.log('a')
bank.log('b')
bank.log('c')
bank.log('a')
bank.log('b')
print(bank.pos(('a','b')))
[0, 3]
[17]:
bank.revert()
[17]:
'b'
[18]:
print(bank)
Bank: a,b,c,a
[19]:
print(bank.pos(('a','b')))
[0]
B2.3 max_interval
Typically, there is a biseq which triggers a period of suspicious activity, and there is another biseq which ends it. So given a start and an end biseq, the bank wants a report of all the transactions that happened in between:
def max_interval(self, bi_start, bi_end):
""" RETURN a list with all the transactions occurred between
the *largest* interval among bi-sequences bi_start and bi_end
- bi_start and bi_end are EXCLUDED
- if bi_start / bi_end are not found, or if bi_end is before/includes bi_start,
raise LookupError
- DO *NOT* MODIFY the data structure
- MUST EXECUTE IN O(k) where k is the length of the *largest* interval
you can return
- consider number of repetitions a negligible size
"""
Testing: python -m unittest bank_test.MaxIntervalTest
Example:
[20]:
bank = Bank()
bank.log('c')
bank.log('d')
bank.log('c')
bank.log('a')
bank.log('b') # <--- b
bank.log('e') # e
bank.log('f') # --- f |
bank.log('a') # a |
bank.log('f') # f | k
bank.log('c') # c |
bank.log('b') # --- b |
bank.log('a') # <--- a
bank.log('f') # f
bank.log('b')
bank.log('e')
bank.log('l')
bank.max_interval( ('b','e'), ('a','f') )
[20]:
['f', 'a', 'f', 'c', 'b']
[ ]: