OOP

Download exercises zip

Browse files online

What to do

• unzip exercises in a folder, you should get something like this:

oop
   complex_number.py
   complex_number_test.py
   complex_number_sol.py
   multiset.py
   multiset_test.py
   multiset_sol.py
   matrix.py
   oop.ipynb
   jupman.py
   sciprog.py

This time you will not write in the notebook, instead you will edit .py files in Visual Studio Code.

Now proceed reading.

1. Abstract Data Types (ADT) Theory

1.1. Intro

• Theory from the slides:

  • Andrea Passerini - Programming paradagims, Object-Oriented Python

• Object Oriented programming on the the book (In particular, Fraction class, in this course we won’t focus on inheritance)

1.2. Complex number theory

1.3. Datatypes the old way

From the definition we see that to identify a complex number we need two float values . One number is for the *real* part, and another number is for the *imaginary* part.

How can we represent this in Python? So far, you saw there are many ways to put two numbers together. One way could be to put the numbers in a list of two elements, and implicitly assume the first one is the real and the second the imaginary part:

c = [3.0, 5.0]

Or we could use a tuple:

c = (3.0, 5.0)

A problem with the previous representations is that a casual observer might not know exactly the meaning of the two numbers. We could be more explicit and store the values into a dictionary, using keys to identify the two parts:

c = {'real': 3.0, 'imaginary': 5.0}

print(c)

{'real': 3.0, 'imaginary': 5.0}

print(c['real'])

3.0

print(c['imaginary'])

5.0

Now, writing the whole record {'real': 3.0, 'imaginary': 5.0} each time we want to create a complex number might be annoying and error prone. To help us, we can create a little shortcut function named complex_number that creates and returns the dictionary:

def complex_number(real, imaginary):
    d = {}
    d['real'] = real
    d['imaginary'] = imaginary
    return d

c = complex_number(3.0, 5.0)

print(c)

{'real': 3.0, 'imaginary': 5.0}

To do something with our dictionary, we would then define functions, like for example complex_str to show them nicely:

def complex_str(cn):
    return str(cn['real']) + " + " + str(cn['imaginary']) + "i"

c = complex_number(3.0, 5.0)
print(complex_str(c))

3.0 + 5.0i

We could do something more complex, like defining the phase of the complex number which returns a float:

IMPORTANT: In these exercises, we care about programming, not complex numbers theory. There’s no need to break your head over formulas!

import math
def phase(cn):
        """ Returns a float which is the phase (that is, the vector angle) of the complex number

            See definition: https://en.wikipedia.org/wiki/Complex_number#Absolute_value_and_argument
        """
        return math.atan2(cn['imaginary'], cn['real'])

c = complex_number(3.0, 5.0)
print(phase(c))

1.0303768265243125

We could even define functions that that take the complex number and some other parameter, for example we could define the log of complex numbers, which return another complex number (mathematically it would be infinitely many, but we just pick the first one in the series):

import math
def log(cn, base):
        """ Returns another complex number which is the logarithm of this complex number

            See definition (accomodated for generic base b):
            https://en.wikipedia.org/wiki/Complex_number#Natural_logarithm
        """
        return {'real':math.log(cn['real']) / math.log(base),
                'imaginary' : phase(cn) / math.log(base)}

print(log(c,2))

{'real': 1.5849625007211563, 'imaginary': 1.4865195378735334}

You see we got our dictionary representing a complex number. If we want a nicer display we can call on it the complex_str we defined:

print(complex_str(log(c,2)))

1.5849625007211563 + 1.4865195378735334i

1.4. Finding the pattern

So, what have we done so far?

1. Decided a data format for the complex number, saw that the dictionary is quite convenient

2. Defined a function to quickly create the dictionary:

   def complex_number(real, imaginary):
   

3. Defined some function like phase and log to do stuff on the complex number

def phase(cn):
def log(cn, base):

4. Defined a function complex_str to express the complex number as a readable string:

def complex_str(cn):

Notice that:

• all functions above take a cn complex number dictionary as first parameter

• the functions phase and log are quite peculiar to complex number, and to know what they do you need to have deep knowledge of what a complex number is.

• the function complex_str is more intuitive, because it covers the common need of giving a nice string representation to the data format we just defined. Also, we used the word str as part of the name to give a hint to the reader that probably the function behaves in a way similar to the Python function str().

When we encounter a new datatype in our programs, we often follow the procedure of thinking listed above. Such procedure is so common that software engineering people though convenient to provide a specific programming paradigm to represent it, called Object Oriented programming. We are now going to rewrite the complex number example using such paradigm.

1.5. Object Oriented Programming

In Object Oriented Programming, we usually:

1. introduce new datatypes by declaring a class, named for example ComplexNumber

2. are given a dictionary and define how data is stored in the dictionary (i.e. in fields real and imaginary)

3. define a way to construct specific instances , like 3 + 2i, 5 + 6i (instances are also called objects)

4. define some methods to operate on the instances (like phase)

5. define some special methods to customize how Python treats instances (for example for displaying them as strings when printing)

Let’s now create our first class.

2. ComplexNumber class

2.1. Class declaration

A minimal class declaration will at least declare the class name and the __init__ method:

class ComplexNumber:

    def __init__(self, real, imaginary):
        self.real = real
        self.imaginary = imaginary

Here we declare to Python that we are starting defining a template for a new class called ComplexNumber. This template will hold a collection of functions (called methods) that manipulate instances of complex numbers (instances are 1.0 + 2.0i, 3.0 + 4.0i, …).

IMPORTANT: Although classes can have any name (i.e. complex_number, complexNumber, …), by convention you SHOULD use a camel cased name like ComplexNumber, with capital letters as initials and no underscores.

2.2. Constructor __init__

With the dictonary model, to create complex numbers remember we defined that small utility function complex_number, where inside we were creating the dictionary:

def complex_number(real, imaginary):
    d = {}
    d['real'] = real
    d['imaginary'] = imaginary
    return d

With classes, to create objects we have instead to define a so-called constructor method called __init__:

class ComplexNumber:

    def __init__(self, real, imaginary):
        self.real = real
        self.imaginary = imaginary

__init__ is a very special method, that has the job to initialize an instance of a complex number. It has three important features:

1. it is defined like a function, inside the ComplexNumber declaration (as usual, indentation matters!)

2. it always takes as first parameter self, which is an instance of a special kind of dictionary that will hold the fields of the complex number. Inside the previous complex_number function, we were creating a dictionary d. In __init__ method, the dictionary instead is automatically created by Python and given to us in the form of parameter self

3. __init__ does not return anything: this is different from the previous complex_number function where instead we were returning the dictionary d.

Later we will explain better these properties. For now, let’s just concentrate on the names of things we see in the declaration.

WARNING: There can be only one constructor method per class, and MUST be named __init__

WARNING: init MUST take at least one parameter, by convention it is usually named self

IMPORTANT: self could be any name!

Self is just a name we give to the first parameter. It could be any name our fantasy suggest and the program would behave exactly the same!

If the editor you are using will evidence it in some special color, it is because it is aware of the convention but not because self is some special Python keyword.

IMPORTANT: In general, any of the __init__ parameters can have completely arbitrary names, so for example the following code snippet would work exactly the same as the initial definition:

class ComplexNumber:

    def __init__(donald_duck, mickey_mouse, goofy):
        donald_duck.real = mickey_mouse
        donald_duck.imaginary = goofy

Once the __init__ method is defined, we can create a specific ComplexNumber instance with a call like this:

c = ComplexNumber(3.0,5.0)
print(c)

<__main__.ComplexNumber object at 0x7f85181f4c90>

What happend here?

init 2.2.1) We told Python we want to create a new particular instance of the template defined by class ComplexNumber. As parameters for the instance we indicated 3.0 and 5.0.

WARNING: you need round parenthesis to create the instance!

We used the name of the class ComplexNumber following it by an open round parenthesis and parameters like a function call: c=ComplexNumber(3.0,5.0)

Writing just c = ComplexNumber would NOT instantiate anything and we would end up messing with the template ComplexNumber, which is a collection of functions for complex numbers.

init 2.2.2) Python created a new special dictionary for the instance

init 2.2.3) Python passed the special dictionary as first parameter of the method __init__, so it will be bound to parameter self. As second and third arguments passed 3.0 and 5.0, which will be bound respectively to parameters real and imaginary

WARNING: You don’t need to pass a dictionary to instantiate a class!

When instantiating an object with a call like c=ComplexNumber(3.0,5.0) you don’t need to pass a dictionary as first parameter! Python will implicitly create it and pass it as first parameter to __init__

init 2.2.4) In the __init__ method, the instructions

self.real = real
self.imaginary = imaginary

first create a key in the dictionary called real associating to the key the value of the parameter real (in the call is 3.0). Then the value 5.0 is bound to the key imaginary.

IMPORTANT: self is special!

We said Python provides __init__ with a special kind of dictionary as first parameter. One of the reason it is special is that you can access keys using the dot like self.my_key. With ordinary dictionaries you would have to write the brackets like self["my_key"]

IMPORTANT: like with dictionaries, we can arbitrarily choose the name of the keys, and which values to associate to them.

IMPORTANT: In the following, we will often refer to keys of the self dictionary with the terms field, and/or attribute.

Now one important word of wisdom:

!!!!!! VIII COMMANDMENT : YOU SHALL NEVER EVER REASSIGN self !!!!!!!

Since self is a kind of dictionary, you might be tempted to do like this:

class EvilComplexNumber:
    def __init__(self, real, imaginary):
        self = {'real':real, 'imaginary':imaginary}

but to the outside world this will bring no effect. For example, let’s say somebody from outside makes a call like this:

ce = EvilComplexNumber(3.0, 5.0)

At the first attempt of accessing any field, you would get an error because after the initalization c will point to the yet untouched self created by Python, and not to your dictionary (which at this point will be simply lost):

print(ce.real)

AttributeError: EvilComplexNumber instance has no attribute ‘real’

In general, you DO NOT reassign self to anything. Here are other example DON’Ts:

self = ['666']  # self is only supposed to be a sort of dictionary which is passed by Python
self = 6        # self is only supposed to be a sort of dictionary which is passed by Python

init 2.2.5) Python automatically returns from __init__ the special dictionary self

WARNING: __init__ must NOT have a return statement !

Python will implicitly return self !

init 2.2.6) The result of the call (so the special dictionary) is bound to external variable ‘c`:

c = ComplexNumber(3.0, 5.0)

init 2.2.7) You can then start using c as any variable

print(c)

<__main__.ComplexNumber object at 0x7f85181f4c90>

From the output, you see we have indeed an instance of the class ComplexNumber. To see the difference between instance and class, you can try printing the class instead:

print(ComplexNumber)

<class '__main__.ComplexNumber'>

IMPORTANT: instances are different from a class

You can create an infinite number of different instances (i.e. ComplexNumber(1.0, 1.0), ComplexNumber(2.0, 2.0), ComplexNumber(3.0, 3.0), … ), but you will have only one class definition for them (ComplexNumber).

We can now access the fields of the special dictionary by using the dot notation as we were doing with the ‘self`:

print(c.real)

3.0

print(c.imaginary)

5.0

If we want, we can also change them:

c.real = 6.0
print(c.real)

6.0

2.3. Defining methods

2.3.1 phase

Let’s make our class more interesting by adding the method phase(self) to operate on the complex number:

import unittest
import math

class ComplexNumber:

    def __init__(self, real, imaginary):
        self.real = real
        self.imaginary = imaginary

    def phase(self):
        """ Returns a float which is the phase (that is, the vector angle) of the complex number

            This method is something we introduce by ourselves, according to the definition:
            https://en.wikipedia.org/wiki/Complex_number#Absolute_value_and_argument
        """
        return math.atan2(self.imaginary, self.real)

The method takes as first parameter self which again is a special dictionary. We expect the dictionary to have already been initialized with some values for real and imaginary fields. We can access them with the dot notation as we did before:

return math.atan2(self.imaginary, self.real)

How can we call the method on instances of complex numbers? We can access the method name from an instance using the dot notation as we did with other keys:

c = ComplexNumber(3.0,5.0)
print(c.phase())

1.0303768265243125

What happens here?

By writing c.phase() , we call the method phase(self) which we just defined. The method expects as first parameter self a class instance, but in the call c.phase() apparently we don’t provide any parameter. Here some magic is going on, and Python implicitly is passing as first parameter the special dictionary bound to c. Then it executes the method and returns the desired float.

WARNING: Put round parenthesis in method calls!

When calling a method, you MUST put the round parenthesis after the method name like in c.phase()! If you just write c.phase without parenthesis you will get back an address to the physical location of the method code:

>>> c.phase
<bound method ComplexNumber.phase of <__main__.ComplexNumber instance at 0xb465a4cc>>

2.3.2 log

We can also define methods that take more than one parameter, and also that create and return ComplexNumber instances, like for example the method log(self, base):

import math

class ComplexNumber:

    def __init__(self, real, imaginary):
        self.real = real
        self.imaginary = imaginary

    def phase(self):
        """ Returns a float which is the phase (that is, the vector angle) of the complex number

            This method is something we introduce by ourselves, according to the definition:
            https://en.wikipedia.org/wiki/Complex_number#Absolute_value_and_argument
        """
        return math.atan2(self.imaginary, self.real)

    def log(self, base):
        """ Returns another ComplexNumber which is the logarithm of this complex number

            This method is something we introduce by ourselves, according to the definition:
            (accomodated for generic base b)
            https://en.wikipedia.org/wiki/Complex_number#Natural_logarithm
        """
        return ComplexNumber(math.log(self.real) / math.log(base), self.phase() / math.log(base))

WARNING: ALL METHODS MUST HAVE AT LEAST ONE PARAMETER, WHICH BY CONVENTION IS NAMED self !

To call log, you can do as with phase but this time you will need also to pass one parameter for the base parameter, in this case we use the exponential math.e:

c = ComplexNumber(3.0, 5.0)
logarithm = c.log(math.e)

WARNING: As before for phase, notice we didn’t pass any dictionary as first parameter! Python will implicitly pass as first argument the instance c as self, and math.e as base

print(logarithm)

<__main__.ComplexNumber object at 0x7f851815cad0>

To see if the method worked and we got back we got back a different complex number, we can print the single fields:

print(logarithm.real)

1.0986122886681098

print(logarithm.imaginary)

1.0303768265243125

2.3.3 __str__ for printing

As we said, printing is not so informative:

print(ComplexNumber(3.0, 5.0))

<__main__.ComplexNumber object at 0x7f851816a5d0>

It would be nice to instruct Python to express the number like “3.0 + 5.0i” whenever we want to see the ComplexNumber represented as a string. How can we do it? Luckily for us, defining the __str__(self) method (see bottom of class definition)

WARNING: There are two underscores _ before and two underscores _ after in __str__ !

import math

class ComplexNumber:

    def __init__(self, real, imaginary):
        self.real = real
        self.imaginary = imaginary

    def phase(self):
        """ Returns a float which is the phase (that is, the vector angle) of the complex number

            This method is something we introduce by ourselves, according to the definition:
            https://en.wikipedia.org/wiki/Complex_number#Absolute_value_and_argument
        """
        return math.atan2(self.imaginary, self.real)

    def log(self, base):
        """ Returns another ComplexNumber which is the logarithm of this complex number

            This method is something we introduce by ourselves, according to the definition:
            (accomodated for generic base b)
            https://en.wikipedia.org/wiki/Complex_number#Natural_logarithm
        """
        return ComplexNumber(math.log(self.real) / math.log(base), self.phase() / math.log(base))

    def __str__(self):
        return str(self.real) + " + " + str(self.imaginary) + "i"

IMPORTANT: all methods starting and ending with a double underscore __ have a special meaning in Python: depending on their name, they override some default behaviour. In this case, with __str__ we are overriding how Python represents a ComplexNumber instance into a string.

WARNING: follow the specs!

Since we are overriding Python default behaviour, it is very important that we follow the specs of the method we are overriding to the letter. In our case, the specs for __str__ obviously state you MUST return a string. Do read them!

c = ComplexNumber(3.0, 5.0)

We can also pretty print the whole complex number. Internally, print function will look if the class ComplexNumber has defined a method named __str__. If so, it will pass to the method the instance c as the first argument, which in our methods will end up in the self parameter:

print(c)

3.0 + 5.0i

print(c.log(2))

1.5849625007211563 + 1.4865195378735334i

Special Python methods are like any other method, so if we wish, we can also call them directly:

c.__str__()

'3.0 + 5.0i'

EXERCISE: There is another method for getting a string representation of a Python object, called __repr__. Read carefully __repr__ documentation and implement the method. To try it and see if any difference appear with respect to str, call the standard Python functions repr and str like this:

c = ComplexNumber(3,5)
print(repr(c))
print(str(c))

QUESTION: Would 3.0 + 5.0i be a valid Python expression ? Should we return it with __repr__? Read again also __str__ documentation

2.4. ComplexNumber code skeleton

We are now ready to write methods on our own. Open Visual Studio Code (no jupyter in part B !) and proceed editing file ComplexNumber.py

To see how to test, try running this in the console, tests should pass (if system doesn’t find python3 write python):

python3 -m unittest complex_number_test.ComplexNumberTest

2.5. Complex numbers magnitude

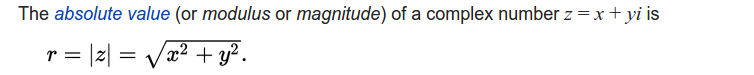
Implement the magnitude method, using this signature:

def magnitude(self):
    """ Returns a float which is the magnitude (that is, the absolute value) of the complex number

        This method is something we introduce by ourselves, according to the definition:
        https://en.wikipedia.org/wiki/Complex_number#Absolute_value_and_argument
    """
    raise Exception("TODO implement me!")

To test it, check this test in MagnitudeTest class passes (notice the almost in assertAlmostEquals !!!):

def test_01_magnitude(self):
    self.assertAlmostEqual(ComplexNumber(3.0,4.0).magnitude(),5, delta=0.001)

To run the test, in the console type:

python3 -m unittest complex_number_test.MagnitudeTest

2.6. Complex numbers equality

Here we will try to give you a glimpse of some aspects related to Python equality, and trying to respect interfaces when overriding methods. Equality can be a nasty subject, here we will treat it in a simplified form.

First of all, try to execute this command, you should get back False

ComplexNumber(1,2) == ComplexNumber(1,2)

False

How comes we get False? The reason is whenever we write ComplexNumber(1,2) we are creating a new object in memory. Such object will get assigned a unique address number in memory, and by default equality between class instances is calculated considering only equality among memory addresses. In this case we create one object to the left of the expression and another one to the right. So far we didn’t tell Python how to deal with equality for ComplexNumber classes, so default equality testing is used by checking memory addresses, which are different - so we get False.

To get True as we expect, we need to implement __eq__ special method. This method should tell Python to compare the fields within the objects, and not just the memory address.

REMEMBER: as all methods starting and ending with a double underscore __, __eq__ has a special meaning in Python: depending on their name, they override some default behaviour. In this case, with __eq__ we are overriding how Python checks equality. Please review __eq__ documentation before continuing.

QUESTION: What is the return type of __eq__ ?

• Implement equality for ComplexNumber more or less as it was done for Fraction

  Use this method signature:

  def __eq__(self, other):
  

  Since __eq__ is a binary operation, here self will represent the object to the left of the ==, and other the object to the right.

Use this simple test case to check for equality in class EqTest:

def test_01_integer_equality(self):
    """
        Note all other tests depend on this test !

        We want also to test the constructor, so in c we set stuff by hand
    """
    c = ComplexNumber(0,0)
    c.real = 1
    c.imaginary = 2
    self.assertEquals(c, ComplexNumber(1,2))

To run the test, in the console type:

python3 -m unittest complex_number_test.EqTest

• Beware ‘equality’ is tricky in Python for float numbers! Rule of thumb: when overriding __eq__, use ‘dumb’ equality, two things are the same only if their parts are literally equal

• If instead you need to determine if two objects are similar, define other ‘closeness’ functions.

• Once done, check again ComplexNumber(1,2) == ComplexNumber(1,2) command and see what happens, this time it should give back True.

QUESTION: What about ComplexNumber(1,2) != ComplexNumber(1,2)? Does it behaves as expected?

• (Non mandatory read) if you are interested in the gory details of equality, see

  • How to Override comparison operators in Python

  • Messing with hashing

2.7. Complex numbers isclose

Complex numbers can be represented as vectors, so intuitively we can determine if a complex number is close to another by checking that the distance between its vector tip and the the other tip is less than a given delta. There are more precise ways to calculate it, but here we prefer keeping the example simple.

Given two complex numbers

\[z_1 = a + bi\]

and

\[z_2 = c + di\]

We can consider them as close if they satisfy this condition:

\[\sqrt{(a-c)^2 + (b-d)^2} < delta\]

• Implement the method in ComplexNumber class:

def isclose(self, c, delta):
    """ Returns True if the complex number is within a delta distance from complex number c.
    """
    raise Exception("TODO Implement me!")

Check this test case IsCloseTest class pass:

def test_01_isclose(self):
    """  Notice we use `assertTrue` because we expect `isclose` to return a `bool` value, and
         we also test a case where we expect `False`
    """
    self.assertTrue(ComplexNumber(1.0,1.0).isclose(ComplexNumber(1.0,1.1), 0.2))
    self.assertFalse(ComplexNumber(1.0,1.0).isclose(ComplexNumber(10.0,10.0), 0.2))

To run the test, in the console type:

python3 -m unittest complex_number_test.IscloseTest

REMEMBER: Equality with __eq__ and closeness functions like isclose are very different things. Equality should check if two objects have the same memory address or, alternatively, if they contain the same things, while closeness functions should check if two objects are similar. You should never use functions like isclose inside __eq__ methods, unless you really know what you’re doing.

2.8. Complex numbers addition

• a and c correspond to real, b and d correspond to imaginary

• implement addition for ComplexNumber more or less as it was done for Fraction in theory slides

• write some tests as well!

Use this definition:

def __add__(self, other):
    raise Exception("TODO implement me!")

Check these two tests pass in AddTest class:

def test_01_add_zero(self):
    self.assertEquals(ComplexNumber(1,2) + ComplexNumber(0,0), ComplexNumber(1,2));

def test_02_add_numbers(self):
    self.assertEquals(ComplexNumber(1,2) + ComplexNumber(3,4), ComplexNumber(4,6));

To run the tests, in the console type:

python3 -m unittest complex_number_test.AddTest

2.9. Adding a scalar

We defined addition among ComplexNumbers, but what about addition among a ComplexNumber and an int or a float?

Will this work?

ComplexNumber(3,4) + 5

What about this?

ComplexNumber(3,4) + 5.0

Try to add the following method to your class, and check if it does work with the scalar:

    def __add__(self, other):
         # checks other object is instance of the class ComplexNumber
        if isinstance(other, ComplexNumber):
            return ComplexNumber(self.real + other.real,self.imaginary + other.imaginary)

        # else checks the basic type of other is int or float
        elif type(other) is int or type(other) is float:
            return ComplexNumber(self.real + other, self.imaginary)

        # other is of some type we don't know how to process.
        # In this case the Python specs say we MUST return 'NotImplemented'
        else:
            return NotImplemented

Hopefully now you have a better add. But what about this? Will this work?

5 + ComplexNumber(3,4)

Answer: it won’t, Python needs further instructions. Usually Python tries to see if the class of the object on left of the expression defines addition for operands to the right of it. In this case on the left we have a float number, and float numbers don’t define any way to deal to the right with your very own ComplexNumber class. So as a last resort Python tries to see if your ComplexNumber class has defined also a way to deal with operands to the left of the ComplexNumber, by looking for the method __radd__ , which means reverse addition . Here we implement it :

def __radd__(self, other):
    """ Returns the result of expressions like    other + self      """
    if (type(other) is int or type(other) is float):
        return ComplexNumber(self.real + other, self.imaginary)
    else:
        return NotImplemented

To check it is working and everything is in order for addition, check these tests in RaddTest class pass:

def test_01_add_scalar_right(self):
    self.assertEquals(ComplexNumber(1,2) + 3, ComplexNumber(4,2));

def test_02_add_scalar_left(self):
    self.assertEquals(3 + ComplexNumber(1,2), ComplexNumber(4,2));

def test_03_add_negative(self):
    self.assertEquals(ComplexNumber(-1,0) + ComplexNumber(0,-1), ComplexNumber(-1,-1));

2.10. Complex numbers multiplication

• Implement multiplication for ComplexNumber, taking inspiration from previous __add__ implementation

• Can you extend multiplication to work with scalars (both left and right) as well?

To implement __mul__, implement definition into ComplexNumber class:

def __mul__(self, other):
    raise Exception("TODO Implement me!")

and make sure these tests cases pass in MulTest class:

def test_01_mul_by_zero(self):
    self.assertEquals(ComplexNumber(0,0) * ComplexNumber(1,2), ComplexNumber(0,0));

def test_02_mul_just_real(self):
    self.assertEquals(ComplexNumber(1,0) * ComplexNumber(2,0), ComplexNumber(2,0));

def test_03_mul_just_imaginary(self):
    self.assertEquals(ComplexNumber(0,1) * ComplexNumber(0,2), ComplexNumber(-2,0));

def test_04_mul_scalar_right(self):
    self.assertEquals(ComplexNumber(1,2) * 3, ComplexNumber(3,6));

def test_05_mul_scalar_left(self):
    self.assertEquals(3 * ComplexNumber(1,2), ComplexNumber(3,6));

3. MultiSet

You are going to implement a class called MultiSet, where you are only given the class skeleton, and you will need to determine which Python basic datastructures like list, set, dict (or combinations thereof) is best suited to actually hold the data.

In math a multiset (or bag) generalizes a set by allowing multiple instances of the multiset’s elements.

The multiplicity of an element is the number of instances of the element in a specific multiset.

For example:

• The multiset a, b contains only elements a and b, each having multiplicity 1

• In multiset a, a, b, a has multiplicity 2 and b has multiplicity 1

• In multiset a, a, a, b, b, b, a and b both have multiplicity 3

NOTE: order of insertion does not matter, so a, a, b and a, b, a are the same multiset, where a has multiplicity 2 and b has multiplicity 1.

from multiset_sol import *

3.1 __init__ add and get

Now implement all of the following methods: __init__, add and get:

def __init__(self):
    """ Initializes the MultiSet as empty."""
    raise Exception("TODO IMPLEMENT ME !!!")

def add(self, el):
    """ Adds one instance of element el to the multiset

        NOTE: MUST work in O(1)
    """
    raise Exception("TODO IMPLEMENT ME !!!")

def get(self, el):
    """ Returns the multiplicity of element el in the multiset.

        If no instance of el is present, return 0.

        NOTE: MUST work in O(1)
    """
    raise Exception("TODO IMPLEMENT ME !!!")

Testing

Once done, running this will run only the tests in AddGetTest class and hopefully they will pass.

Notice that multiset_test is followed by a dot and test class name .AddGetTest :

python3 -m unittest multiset_test.AddGetTest

3.2 removen

Implement the following removen method:

def removen(self, el, n):
    """ Removes n instances of element el from the multiset (that is, reduces el multiplicity by n)

        If n is negative, raises ValueError.
        If n represents a multiplicity bigger than the current multiplicity, raises LookupError

        NOTE: multiset multiplicities are never negative
        NOTE: MUST work in O(1)
    """

Testing: python3 -m unittest multiset_test.RemovenTest

4. Challenges

Have a look at the OOP Matrix Challenge